Unit conversion

Subscribe to R-bloggers already

I have R-bloggers in my News Reader. A while ago the authors of the package announced units on R-bloggers.

I had my formula in science units, my head in a mess of units, but I remembered that I spotted units had been released.

Back to energy spent cycling

A first stab at making that formula as a function:

power = function(v, 
                 g=9.81, 
                 m=90, 
                 k_1=0.0053, 
                 k_2=0.26,
                 s=0){
  g * m * v * (k_1 + s) + k_2 * v^3
} 

power(5.4)

## [1] 66.20924

I simplified it a bit by saying v_a = v_g. And we’ve replicated their example.

If I do the sums, then apply units I can look at a speed-power curve:

tibble(speed = seq(0, 11, length.out= 100)) %>% 
  mutate(power = power(speed)) %>% 
  mutate(speed = set_units(speed, "m/s")) %>% 
  mutate(power = set_units(power, "watts")) %>% 
  mutate(speed = set_units(speed, "miles/hour")) %>% #SI to thinking in road speed
  mutate(power = set_units(power, "kcal/hour")) %>% #SI to human-level energy units
  ggplot(aes(x=speed, y=power)) + geom_line()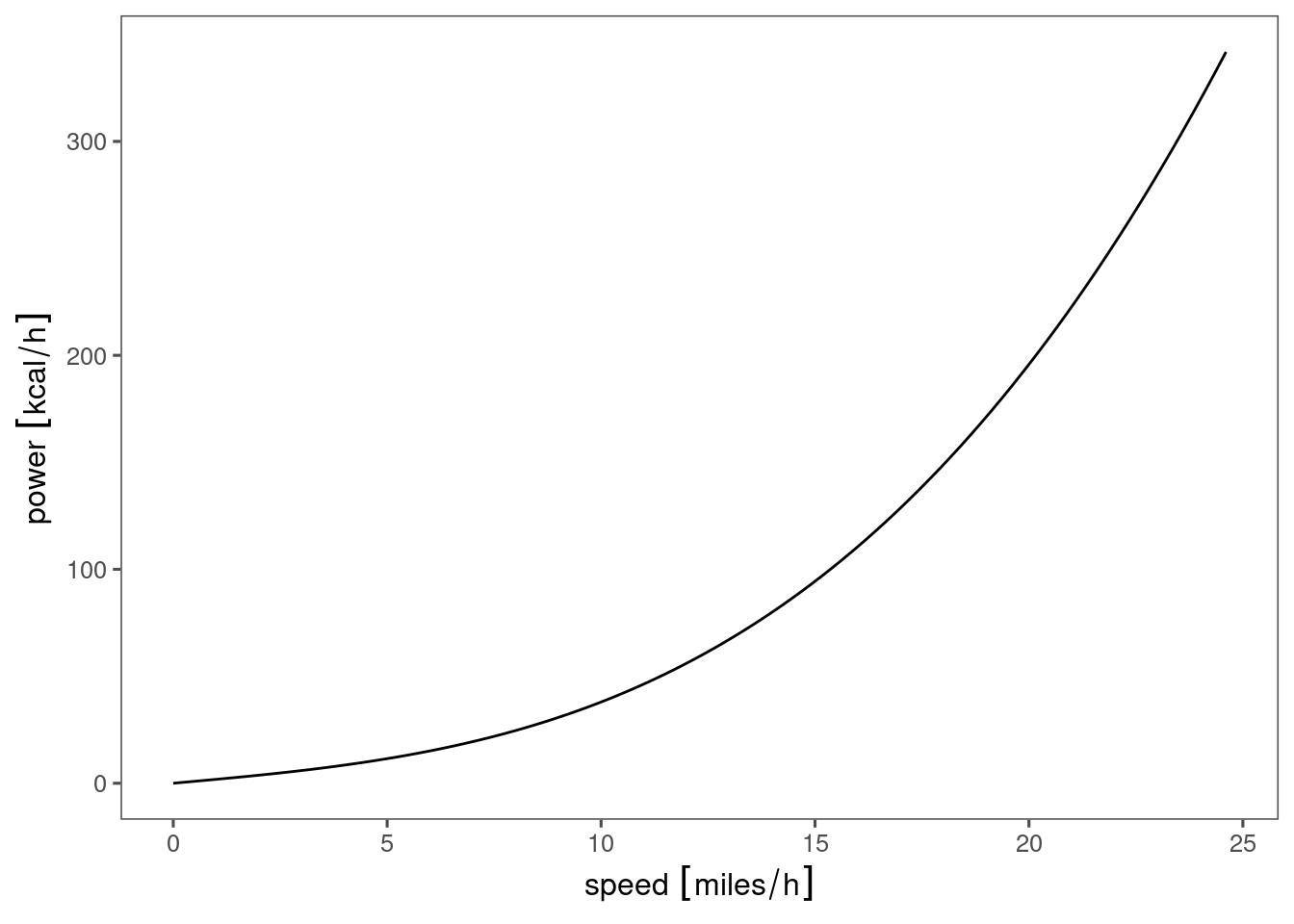

This is after I tried starting with speed in miles/h and converting to m/s. It didn’t like that because the units are incompatible.

This is great! Sensible errors are better than producing nonsensical output, so let’s rewrite the function including a statement that most of these parameters have dimension.

power = function(v, 
                 g=9.81, 
                 m=90, 
                 k_1=0.0053, 
                 k_2=0.26,
                 s=0){
  units(v) <- "m/s"
  units(g) <- "m/s^2"
  units(m) <- "kg"
  units(k_1) <- 1
  units(k_2) <- "kg/m"
  units(s) <- 1
  set_units(g * m * v * (k_1 + s) + k_2 * v^3, "watts")
} 

Then what I wanted for the above example is:

tibble(speed = seq(0, 25, length.out = 100)) %>% #I think this is clearer as 2 lines 
  mutate(speed = set_units(speed, "miles/hour")) %>% 
  mutate(power = power(speed)) %>% 
  mutate(power = set_units(power, "kcal/hour")) %>% 
  ggplot(aes(x=speed, y=power)) + geom_line()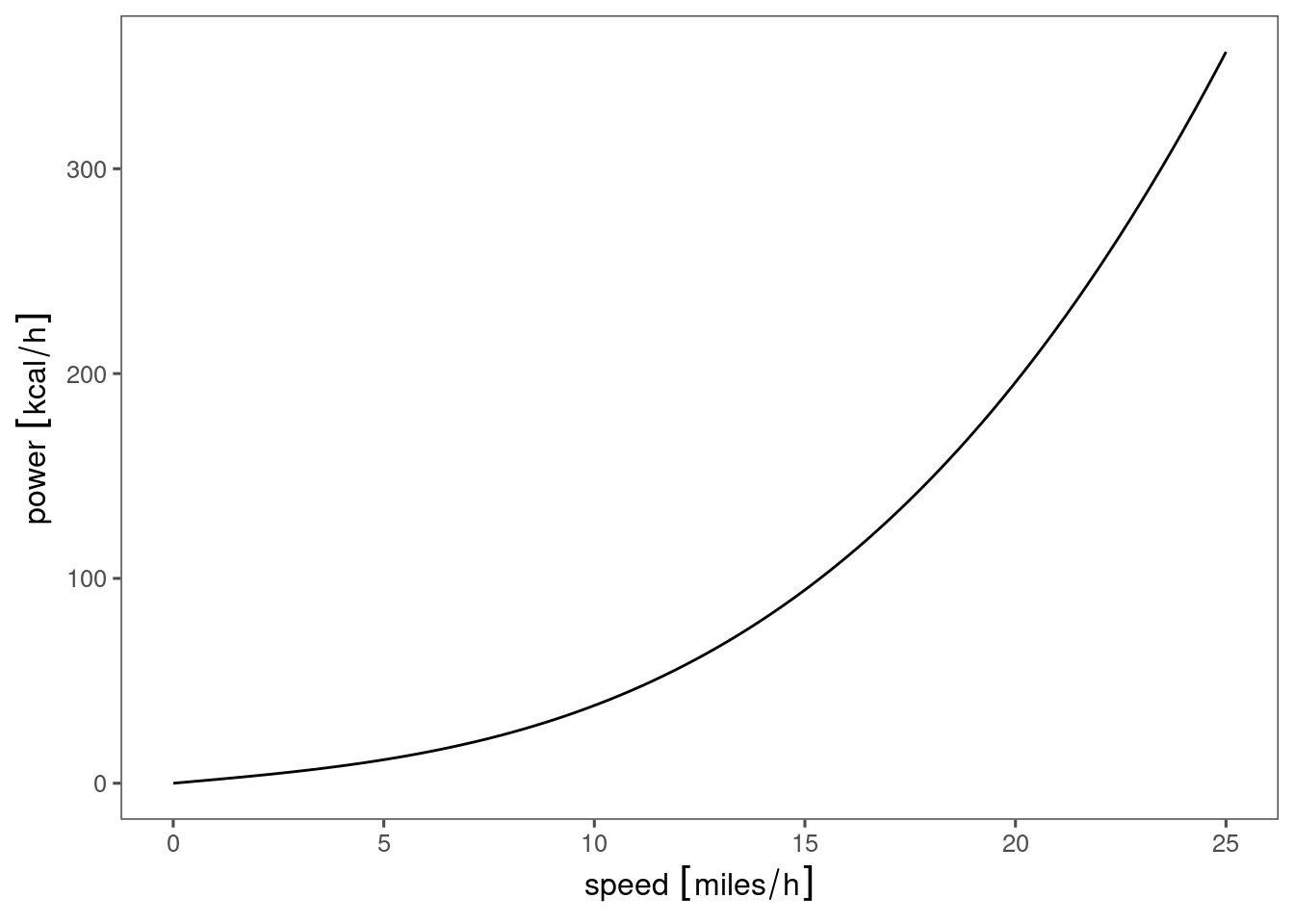

Other graphs

I read Sustainable Energy Without the Hot Air, which suggested in general that moving slower is more energy efficient for distance. ¹

I scribbled on my notepad:

I have:

• speed \(\frac{m}{s}\)
• power \(\frac{j}{s}\)

I want:

• energy per distance \(\frac{j}{m} = \frac{j}{s} \div \frac{m}{s} = \frac{\text{power}}{\text{speed}}\)

So the dimensional analysis helped me work out what sums I wanted to do.

tibble(speed = seq(0, 25, length.out = 1000)) %>% #I think this is clearer as 2 lines 
  mutate(speed = set_units(speed, "miles/hour")) %>% 
  mutate(power = power(speed)) %>% 
  mutate(energy_per_dist = power/speed) %>% 
  mutate(energy_per_dist = set_units(energy_per_dist, "kcal/mile")) %>% 
  ggplot(aes(x=speed, y=energy_per_dist)) + geom_line() +
  ggforce::scale_y_unit(breaks = c(0,5,10,15)) + expand_limits(y=c(0,15))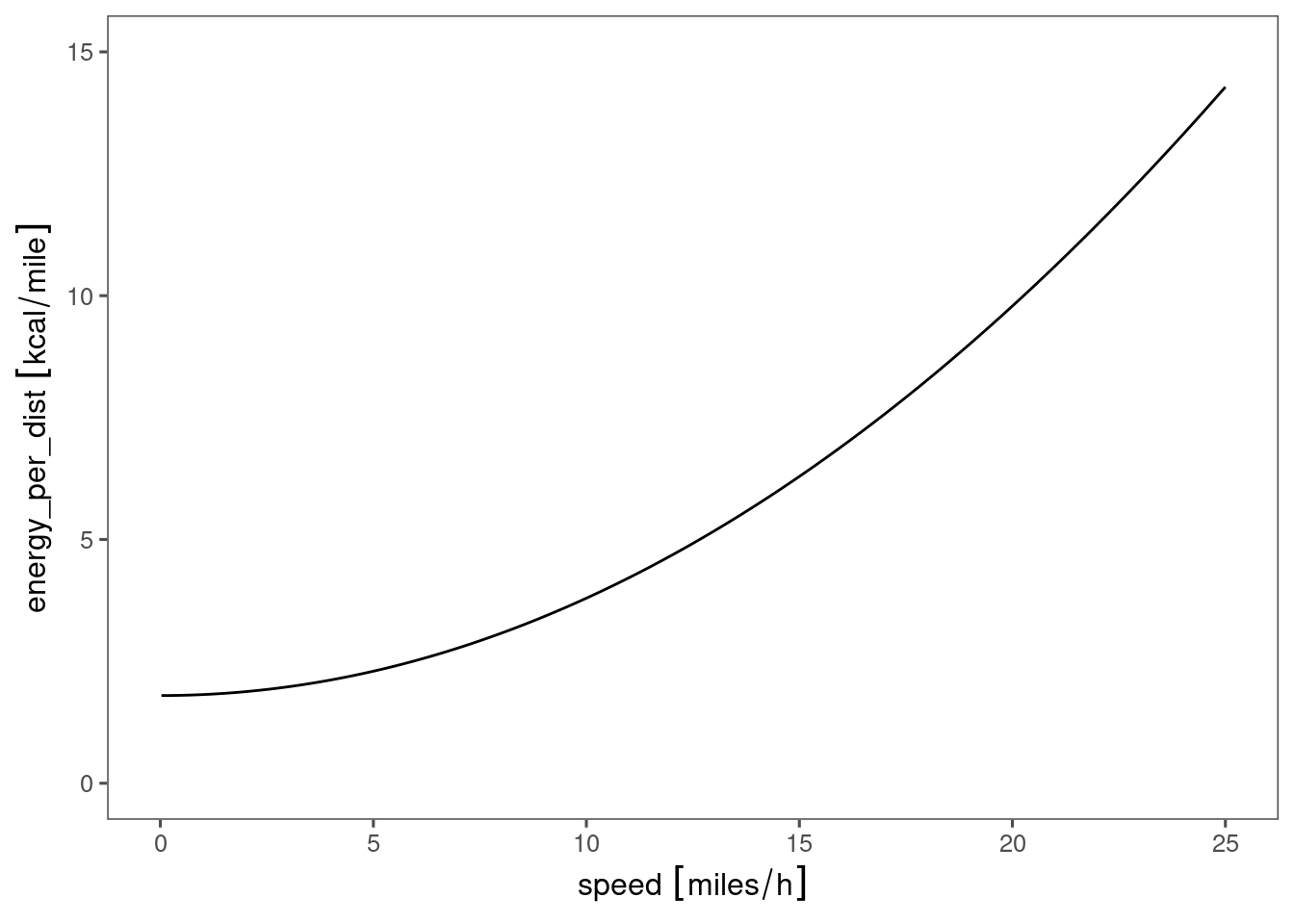

Or using “fat is 9kcal/gram”:

tibble(speed = seq(0, 20, length.out = 1000)) %>% 
  mutate(speed = set_units(speed, "miles/hour")) %>% 
  mutate(power = power(speed)) %>% 
  mutate(energy_per_dist = power/speed) %>% 
  mutate(energy_per_dist = set_units(energy_per_dist, "kcal/mile")) %>% 
  mutate(fat_burned = energy_per_dist / as_units(9, "kcal/g")) %>% 
  mutate(fat_burned = set_units(fat_burned, "g/Mm")) %>% 
  ggplot(aes(x=speed, y=fat_burned)) + geom_line() +
  expand_limits(y=0)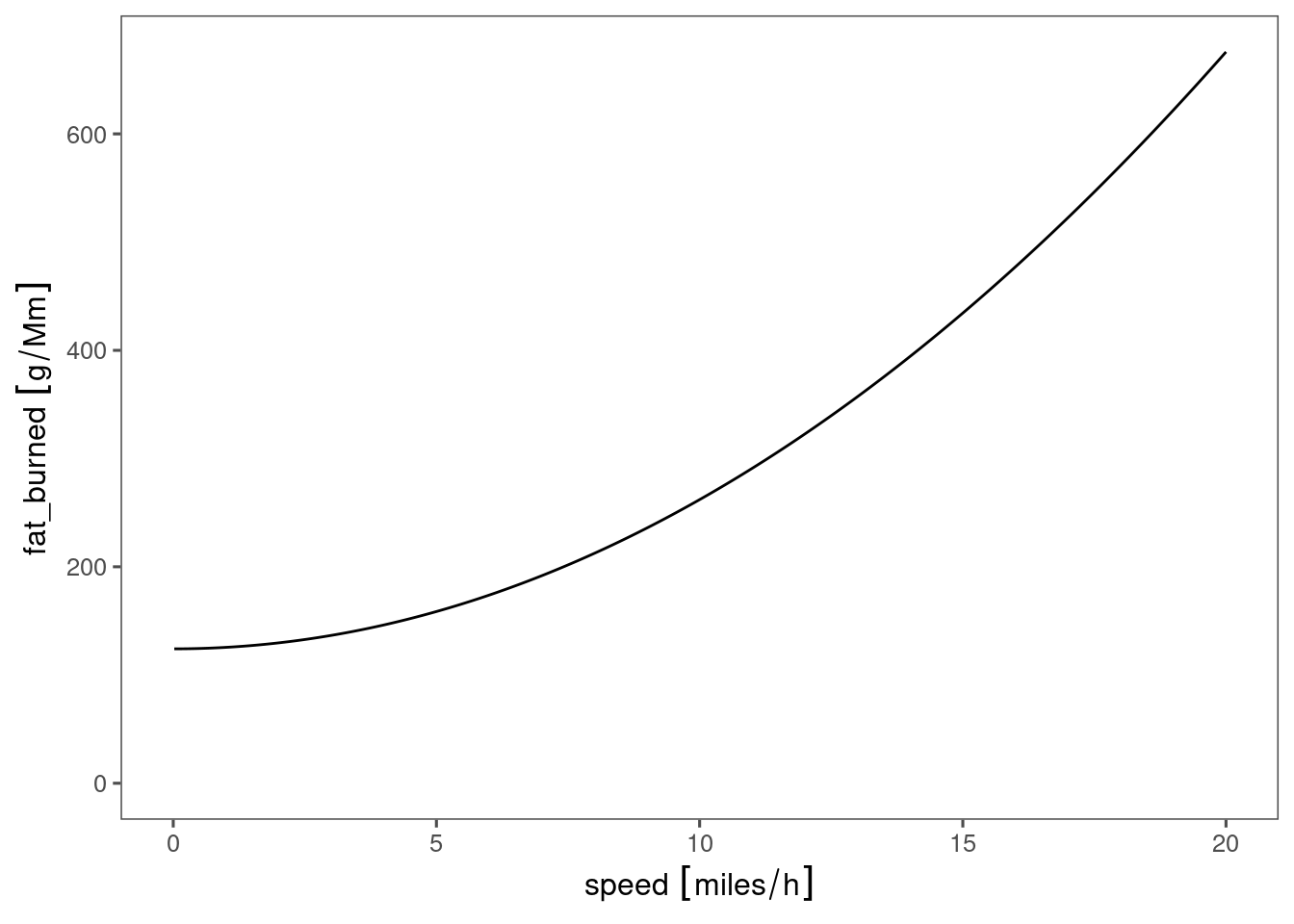

“Mm” being “mega-meters”, or 1000 km. Somewhere in the region of 40 office commutes = 1Mm, for me. I suppose this reinforces the truism that one does cardio to improve their cardiovascular health, not for the energy deficit!

Conclusion

• The {units} package can simplify a bunch of analysis, directly by handling conversion, and indirectly by pointing out that you’re trying to add meters and seconds.
• Cycling can be part of my weight loss, but not the whole story.