FiveThirtyEight Riddler 2019/12/06

Today’s Riddler has a problem - you have a music player with 100 songs, and can only seek a song with “next” and “random”. “random” chooses a number uniformly in 1:100, next is track + 1, and 100 wraps back around to 1. You’ve started on a random track, and want to get to track 42, with as few presses as possible.

In extreme, you could only press “next”. This would cost between 0 and 100 presses, or 50 on average. You could press “random” until your d100 rolls a 42, i.e. least n for which \(1-(.99)^n>0.5\), or 69 randoms on average.

These both put an upper bound on the best answer. I was going to throw genetic evolution at this problem, but when considering what the genes would be I think I solved it.

All that matters is the current state of the machine, if I’m currently on track 99 then it doesn’t matter that my last track was 50, for example. So our genetic program would only be interested in the current track, and from that alone it would decide what to do. There are 99 wrong tracks, and only 1 winning track, so there are \(2^{99}\) algorithms in this space! (6e29…)

But if you’re on track 41, you wouldn’t press “random”, you’d press “next”, and win. If you’re on track 40 then you have a 1/100 probability of being on a better position (track 42 itself) than just pressing “next” (track 41). So we can reduce the \(2^{99}\) algorithms to 100 according to when you believe you’re better off pressing “random” than “next”.

There definitely is a point where pressing “random” is better than pressing “next”. If you are on track 43 then pressing “next” puts you on track 44, at distance 98 from 42. Pressing “random” should put you somewhere near distance 50 on average from 42, so approximately, when the distance to track 42 is less than 50 you should press “next”, and when the distance is greater than 50 press “random”.

I want to test this so let’s write some code.

I’m renumbering this to make the code easier. Desired track is 0, tracks are 0-99. Now “next” is the best strategy above somewhere near 50.

discrete_uniform <- function(n){
  floor(runif(n, 0, 100))
}

action <- function(current_track, gene){
  if_else(current_track > gene, 
          (current_track+1) %% 100,
          discrete_uniform(1)
          )
}

score_once <- function(gene){
  actions <- 0
  current_track <- discrete_uniform(1)
  
  while(current_track != 0){
    actions <- actions+1
    current_track <- action(current_track, gene)
  }
  return(actions)
  
}

genes <- rep(1:100, 1000)

scores <- map_dbl(genes, score_once)

result_table <- tibble(gene=genes, score=scores)
rm(genes, scores)

result_table %>%
  group_by(gene) %>%
  summarise(score=mean(score)) %>%
  ggplot(aes(x=gene,y=score)) + geom_point() + scale_y_continuous(limits = c(0,NA)) + ggthemes::theme_tufte() +
  labs(y="average score")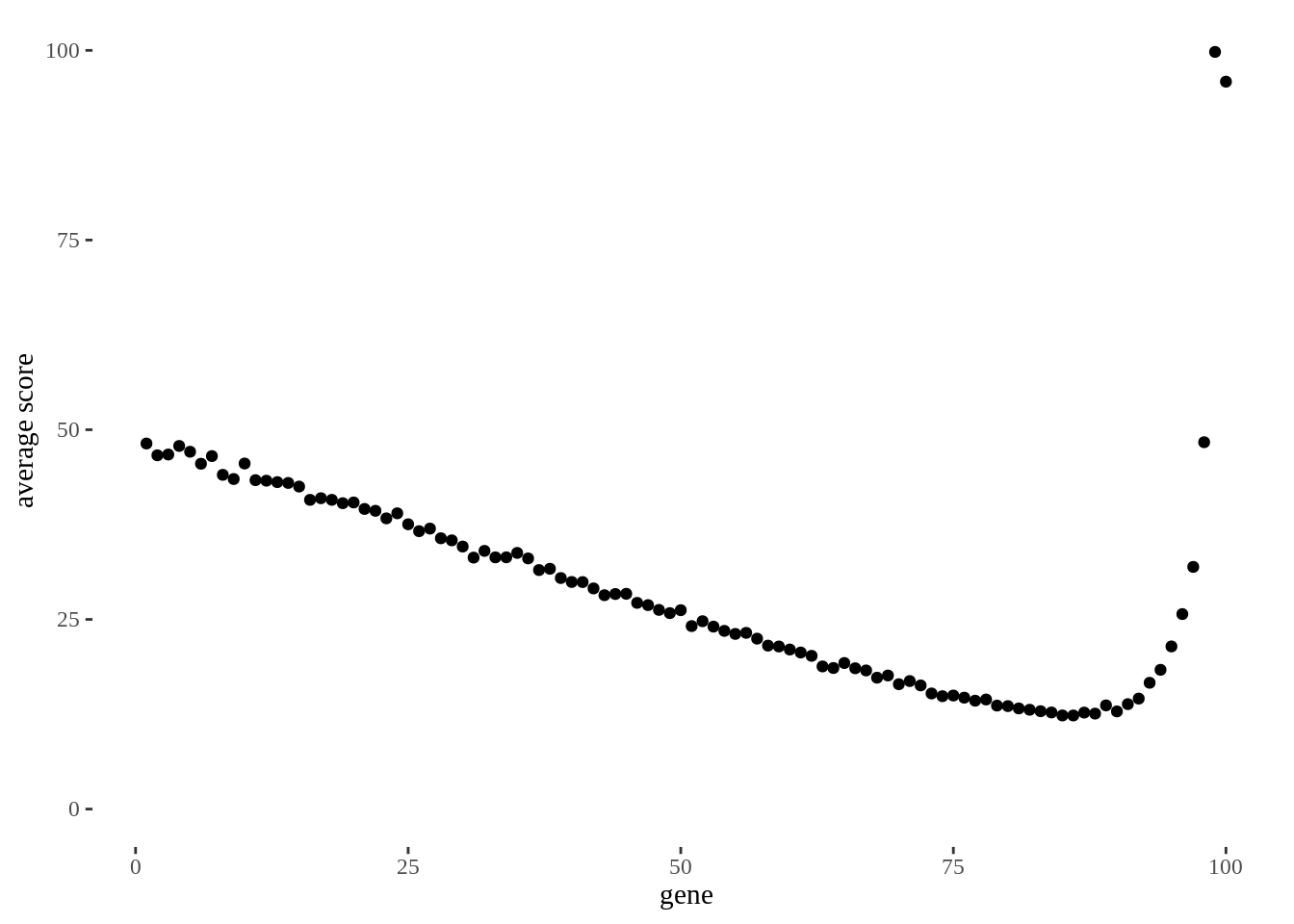

My gut understanding of probability was wrong, which is why Monte Carlo testing it is especially useful for me. In this experient the best, on average was:

result_table %>%
  group_by(gene) %>%
  summarise(score=mean(score)) %>%
  top_n(-1, score) %>%
  knitr::kable()

gene	score
86	12.337

So if you’re on track 87 or higher, hit “next”, otherwise hit “random”. Or in the real example, if you’re on tracks 29-41, press next, otherwise press random.