I was reading one of Ian Stewart’s books of popular maths, and I found a potentially incomplete solution to a puzzle.
Given the (English) Scrabble tile set, do any numbers give their own score?
“One” certainly doesn’t, since “O”,“N”,“E”each score 1 point, and .
For various reasons, you can see that you don’t need to test every number:
- Scrabble scores are non-negative integers.
- Score increases as word length increases. The length of the name of a number increases approximately by powers of ten. (Or logarithmically.)
So “zero”, “one”, score more points than their number, while “one thousand” definitely scores less than itself. (And there’s no word separator in Scrabble. Anyway “thousand” definitely scores less than 1000 points.) Somewhere in the middle we might get some wins?
Code
We just need a function that turns a number into a word and into a scrabble score.
scores <- tibble(
letters = letters,
score = c(
1, 3, 3,
2, 1, 4,
2, 4, 1,
8, 5, 1,
3, 1, 1,
3, 10, 1,
1, 1, 1,
4, 4, 8,
4, 10
)
)
convert_word_to_score <- function(word) {
suppressMessages(str_to_lower(word) %>%
str_extract_all("[a-z]") %>%
unlist() %>%
tibble(letters = .) %>%
left_join(scores) %>%
pull(score) %>%
sum())
}Giving it a try:
convert_word_to_score("one")
## [1] 3I’ve grabbed names for numbers off Wiki, so let’s make a table. (Copy paste is way easier in this case than messing around with scrapes or wiki API.)
base_scores <- tribble(
~number, ~name,
0, "Zero",
1, "One",
2, "Two",
3, "Three",
4, "Four",
5, "Five",
6, "Six",
7, "Seven",
8, "Eight",
9, "Nine",
10, "Ten",
11, "Eleven",
12, "Twelve",
13, "Thirteen",
14, "Fourteen",
15, "Fifteen",
16, "Sixteen",
17, "Seventeen",
18, "Eighteen",
19, "Nineteen",
20, "Twenty"
) %>%
rowwise() %>%
mutate(score = convert_word_to_score(name))
filter(base_scores, number == score) %>%
knitr::kable()| number | name | score |
|---|---|---|
| 12 | Twelve | 12 |
Fortunately, my results match Prof. Stewart’s - “Twelve” scores 12 points.
(Let’s do a few plots…
base_scores %>%
ggplot(aes(x = number, y = score, colour=(number==score))) + geom_point() + geom_line(aes(x = 0:20, y = 0:20, colour=TRUE)) + theme + ggtitle("Twelve is the only number with its own Scrabble score", subtitle = "Line y=x added") + guides(colour=FALSE) + scale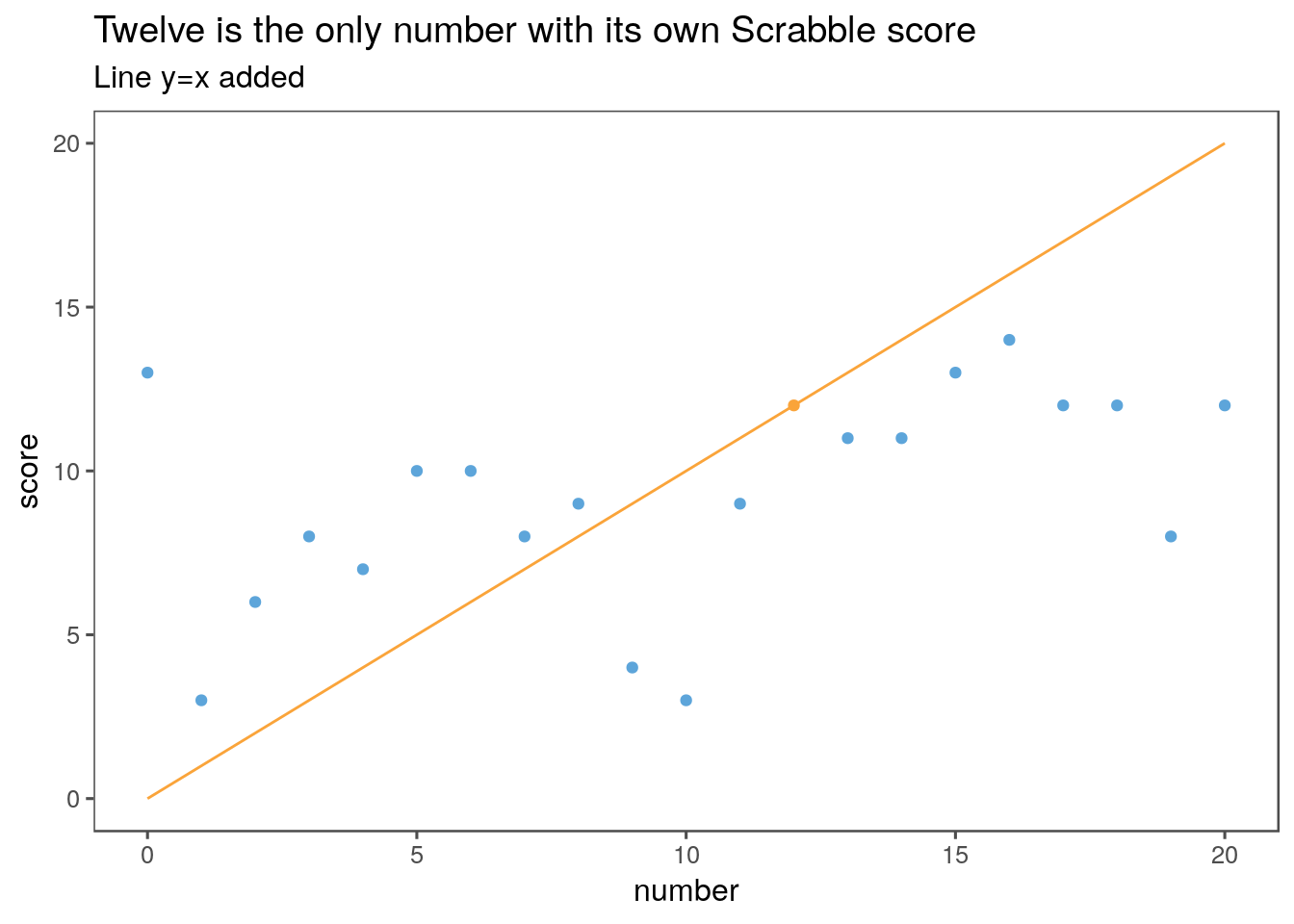 And:
And:
base_scores %>%
filter(number > 0) %>% # Whoops, don't divide by zero.
mutate(relative_score = score / number) %>%
ggplot(aes(x = number, y = relative_score, colour=as.factor(sign(relative_score-1)))) + geom_point() + theme + geom_line(aes(x=1:20,y=1,colour="0")) + labs(
title = "Small numbers score greater than themselves\n
but large numbers smaller.",
y = "Score/number"
) + guides(colour=FALSE) + scale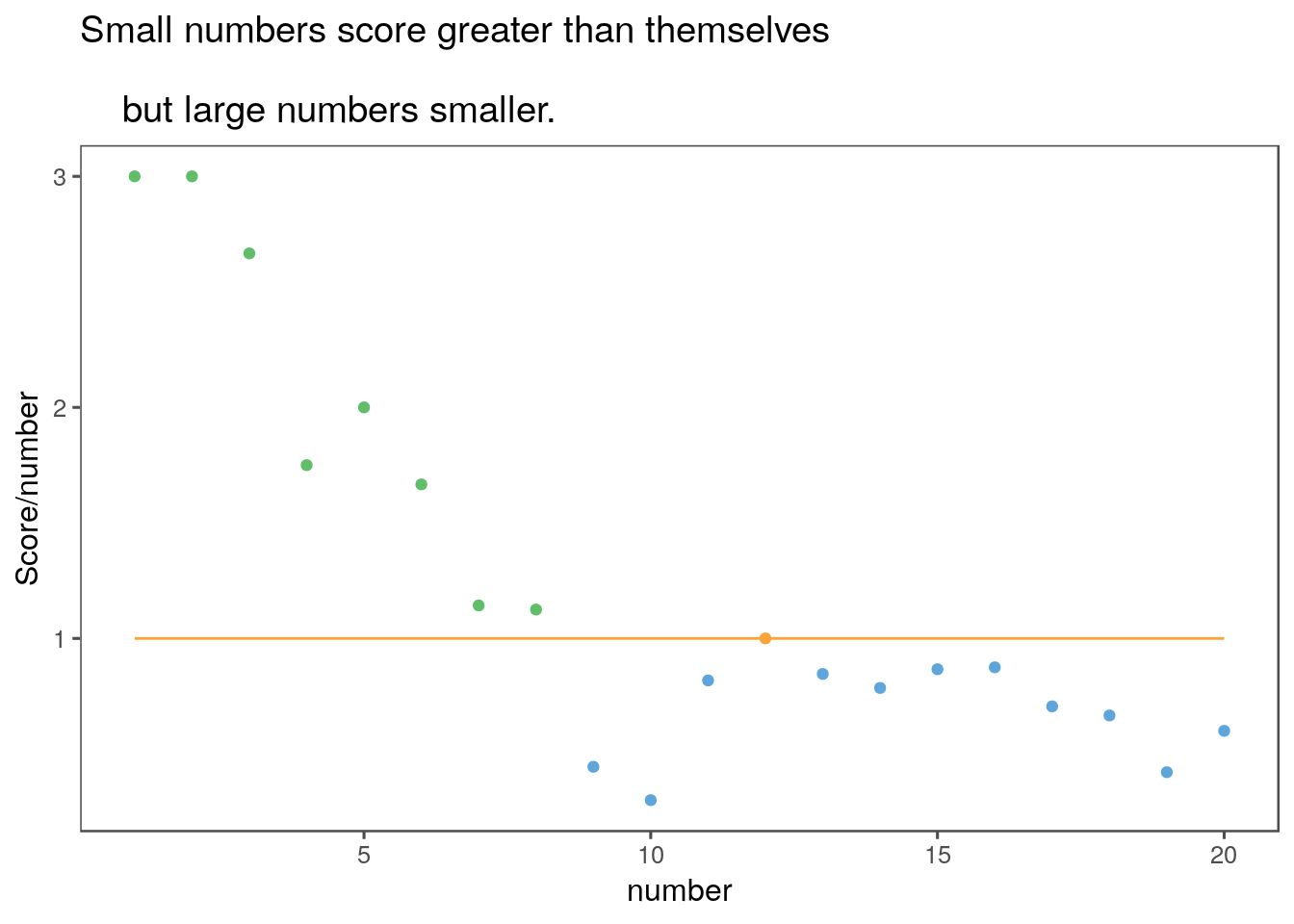 )
)
I attack this puzzle from two additional angles:
- Numbers have more than one name in English.
- There are many ways to modify the base score in Scrabble. (blank tile, letter multipliers, word multipliers…)
Additional names
“Twelve” wins, but “Dozen” scores 15, and . This could push us into another couple of winning words.
Apologies for the massive table. DT doesn’t work with the theme I’m trying now, and I’ve not got it working yet.
alias_scores <- read_csv(here::here("static", "data", "Wiki", "names_of_numbers.csv")) %>%
separate(3, as.character(1:100), ",") %>%
gather("key", "name", -Number) %>%
select(-key) %>%
drop_na() %>%
mutate(name = str_extract(name, "[a-zA-Z \\-]+")) %>% # Too many footnotes and references to countries that need dropping
drop_na() %>%
rowwise() %>%
mutate(score = convert_word_to_score(name)) %>%
arrange(Number)
knitr::kable(alias_scores, rownames = F)| Number | name | score |
|---|---|---|
| 0 | Zero | 13 |
| 0 | aught | 9 |
| 0 | cipher | 13 |
| 0 | cypher | 16 |
| 0 | donut | 6 |
| 0 | dot | 4 |
| 0 | duck | 11 |
| 0 | goose egg | 11 |
| 0 | love | 7 |
| 0 | nada | 5 |
| 0 | naught | 10 |
| 0 | nil | 3 |
| 0 | none | 4 |
| 0 | nought | 10 |
| 0 | nowt | 7 |
| 0 | null | 4 |
| 0 | ought | 9 |
| 0 | oh | 5 |
| 0 | squat | 14 |
| 0 | zed | 13 |
| 0 | zilch | 19 |
| 0 | zip | 14 |
| 0 | zippo | 18 |
| 0 | Sunya | 8 |
| 1 | One | 3 |
| 1 | ace | 5 |
| 1 | individual | 15 |
| 1 | single | 7 |
| 1 | singleton | 10 |
| 1 | unary | 8 |
| 1 | unit | 4 |
| 1 | unity | 8 |
| 1 | Pratham | 14 |
| 2 | Two | 6 |
| 2 | binary | 11 |
| 2 | brace | 9 |
| 2 | couple | 10 |
| 2 | couplet | 11 |
| 2 | distich | 13 |
| 2 | deuce | 8 |
| 2 | double | 9 |
| 2 | doubleton | 12 |
| 2 | duad | 6 |
| 2 | duality | 11 |
| 2 | duet | 5 |
| 2 | duo | 4 |
| 2 | dyad | 9 |
| 2 | pair | 6 |
| 2 | span | 6 |
| 2 | twain | 8 |
| 2 | twin | 7 |
| 2 | twosome | 12 |
| 2 | yoke | 11 |
| 3 | Three | 8 |
| 3 | deuce-ace | 13 |
| 3 | leash | 8 |
| 3 | set | 3 |
| 3 | tercet | 8 |
| 3 | ternary | 10 |
| 3 | ternion | 7 |
| 3 | terzetto | 17 |
| 3 | threesome | 14 |
| 3 | tierce | 8 |
| 3 | trey | 7 |
| 3 | triad | 6 |
| 3 | trine | 5 |
| 3 | trinity | 10 |
| 3 | trio | 4 |
| 3 | triplet | 9 |
| 3 | troika | 10 |
| 3 | hat-trick | 17 |
| 4 | Four | 7 |
| 4 | foursome | 13 |
| 4 | quadruplet | 22 |
| 4 | quatern | 16 |
| 4 | quaternary | 22 |
| 4 | quaternity | 22 |
| 4 | quartet | 16 |
| 4 | tetrad | 7 |
| 5 | Five | 10 |
| 5 | cinque | 17 |
| 5 | fin | 6 |
| 5 | fivesome | 16 |
| 5 | pentad | 9 |
| 5 | quint | 14 |
| 5 | quintet | 16 |
| 5 | quintuplet | 21 |
| 6 | Six | 10 |
| 6 | half dozen | 25 |
| 6 | hexad | 16 |
| 6 | sestet | 6 |
| 6 | sextet | 13 |
| 6 | sextuplet | 18 |
| 6 | sise | 4 |
| 7 | Seven | 8 |
| 7 | heptad | 12 |
| 7 | septet | 8 |
| 7 | septuple | 12 |
| 7 | walking stick | 26 |
| 8 | Eight | 9 |
| 8 | octad | 8 |
| 8 | octave | 11 |
| 8 | octet | 7 |
| 8 | octonary | 13 |
| 8 | octuplet | 12 |
| 8 | ogdoad | 9 |
| 9 | Nine | 4 |
| 9 | ennead | 7 |
| 10 | Ten | 3 |
| 10 | deca | 7 |
| 10 | decade | 10 |
| 10 | das | 4 |
| 11 | Eleven | 9 |
| 11 | onze | 13 |
| 11 | ounze | 14 |
| 11 | ounce | 7 |
| 11 | banker | 12 |
| 12 | Twelve | 12 |
| 12 | dozen | 15 |
| 13 | Thirteen | 11 |
| 13 | baker | 11 |
| 13 | long dozen | 20 |
| 14 | Fourteen | 11 |
| 15 | Fifteen | 13 |
| 16 | Sixteen | 14 |
| 17 | Seventeen | 12 |
| 18 | Eighteen | 12 |
| 19 | Nineteen | 8 |
| 20 | Twenty | 12 |
| 20 | score | 7 |
| 21 | Twenty-one | 15 |
| 21 | long score | 12 |
| 22 | Twenty-two | 18 |
| 22 | Deuce-deuce | 16 |
| 23 | Twenty-three | 20 |
| 24 | Twenty-four | 19 |
| 24 | two dozen | 21 |
| 25 | Twenty-five | 22 |
| 26 | Twenty-six | 22 |
| 27 | Twenty-seven | 20 |
| 28 | Twenty-eight | 21 |
| 29 | Twenty-nine | 16 |
| 30 | Thirty | 12 |
| 31 | Thirty-one | 15 |
| 32 | Thirty-two | 18 |
| 40 | Forty | 11 |
| 40 | two-score | 13 |
| 50 | Fifty | 14 |
| 50 | half-century | 22 |
| 60 | Sixty | 15 |
| 60 | three-score | 15 |
About here I realised I need to get better at tidyr, so I dropped into the manual. There might be a better way with purrr, but I liked turning this into tidy data, particularly because I can chuck it at ggplot again.
Anyway, did I get more solutions?
alias_scores %>%
filter(Number==score) %>%
knitr::kable()| Number | name | score |
|---|---|---|
| 3 | set | 3 |
| 6 | sestet | 6 |
| 8 | octad | 8 |
| 10 | decade | 10 |
| 12 | Twelve | 12 |
Sweet, I expanded the solution space 5x!
Let’s have another look at score relative to number:
alias_scores %>%
filter(Number > 0) %>%
mutate(relative_score = score / Number) %>%
ggplot(aes(x = Number, y = relative_score,
colour=as.factor(sign(relative_score-1)))) + geom_point() + theme + geom_line(aes(x=c(1:60, rep(60,67)),y=1,colour="0")) + labs(
title = "There are more winning numbers if we take other common name",
y = "Score/Number"
) + scale + guides(colour=FALSE)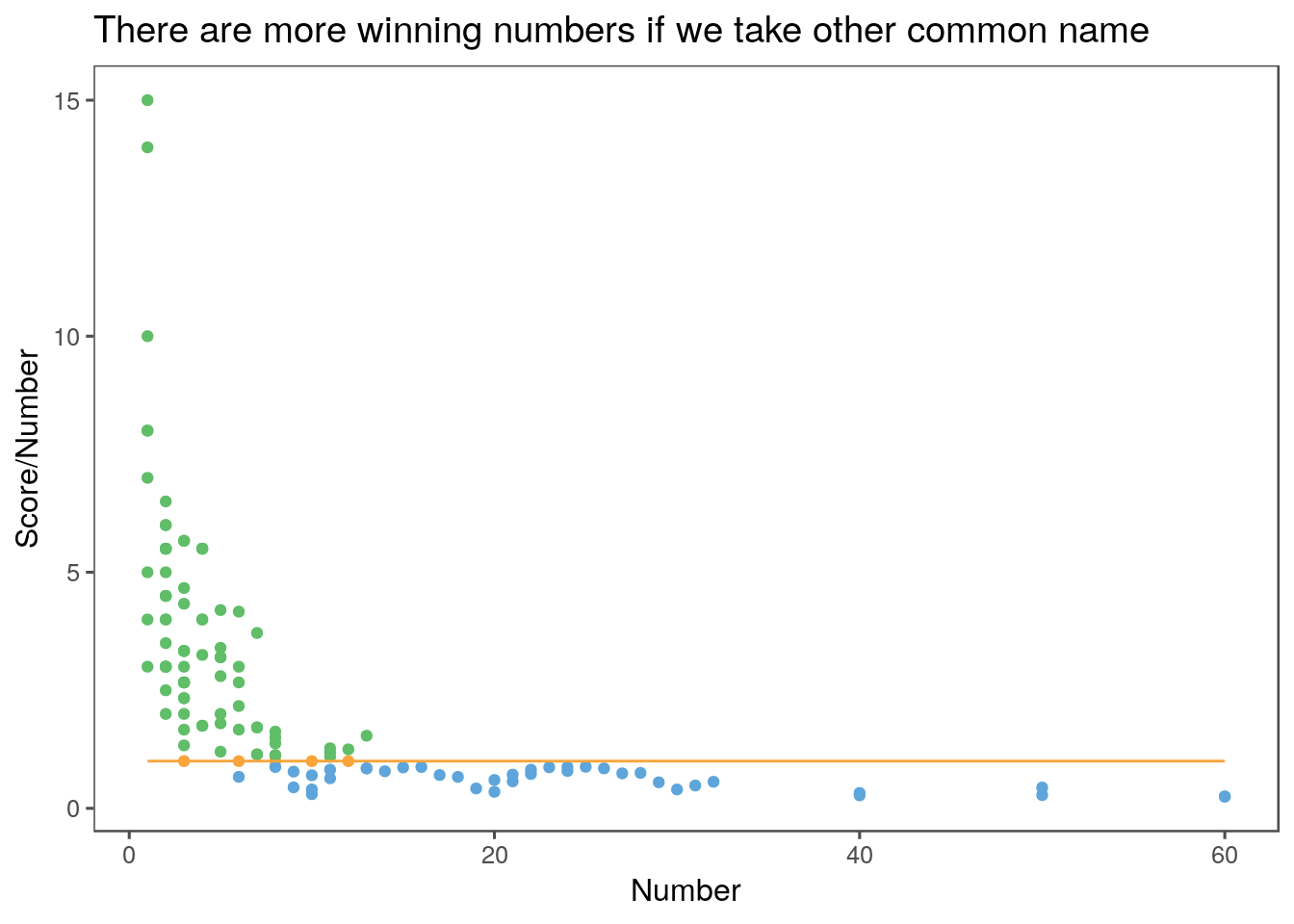
Score modifications
Part 1: the blank tile
Quite a few of the early numbers score more than their value. We might get some of these to turn into winners if we replace some of their letters with the blank tile. This is allowed to substitute any letter, but gives no score.
Right now I’m not going to worry about the actual number of blanks in a Scrabble set, and allow myself as many blank tiles as I want. (Which was implicit in the earlier stuff with the actual letters.)
I need to modify the function that makes a score so it can accept modifiers. In this case, the zero multiplier on a given tile:
word_to_score <- function(word, modifier = 1) {
# I am terrible at writing vectorised functions.
if (class(modifier) == "list") modifier <- unlist(modifier)
suppressMessages(str_to_lower(word) %>%
str_extract_all("[a-z]") %>%
unlist() %>%
tibble(letters = ., modifier = modifier) %>%
left_join(scores) %>%
summarise(score = sum(score * modifier)) %>%
pull())
}The hiliarious thing is that for a word of length , I have to work out ways you can fill it in with blank tiles. At least I know this will only decrease the score, so I can start with the ones who over-scored.
I’m not sure about generating all the binary codes with the word’s length, so I recursed. For a small time save, I generate them all now.
binary <- list(crossing(0:1))
for (i in 2:12) {
binary <- append(
binary,
list(
crossing(binary[[i - 1]], 0:1)
)
)
}
binary <- map(binary, transpose) %>%
flatten() %>%
tibble(sequence = .) %>%
rowwise() %>%
mutate(length = length(sequence)) %>%
ungroup()Now I can slap these sequences on the words that over-scored. As I mentioned above, the solutions for 0 are boring, since they are all blank tiles, so I’m filtering them out.
blank_scores <- alias_scores %>%
mutate(name = name %>%
str_to_lower() %>%
str_remove_all("\\W")) %>%
filter(score > Number) %>%
mutate(length = str_length(name)) %>%
left_join(binary) %>%
rowwise() %>%
mutate(score_with_blanks = word_to_score(name, sequence))
blank_scores %>%
select(Number, name, score_with_blanks) %>%
filter(Number == score_with_blanks) %>%
unique() %>%
group_by(Number) %>%
summarise(name = str_flatten(name, " , ")) %>%
dplyr::arrange(Number) %>%
knitr::kable()| Number | name |
|---|---|
| 0 | zero , aught , cipher , cypher , donut , dot , duck , gooseegg , love , nada , naught , nil , none , nought , nowt , null , ought , oh , squat , zed , zilch , zip , zippo , sunya |
| 1 | one , ace , individual , single , singleton , unary , unit , unity , pratham |
| 2 | two , binary , brace , couple , couplet , distich , deuce , double , doubleton , duad , duality , duet , duo , dyad , pair , span , twain , twin , twosome , yoke |
| 3 | three , deuceace , leash , tercet , ternary , ternion , terzetto , threesome , tierce , trey , triad , trine , trinity , trio , triplet , troika , hattrick |
| 4 | four , foursome , quadruplet , quatern , quaternary , quaternity , quartet , tetrad |
| 5 | five , cinque , fin , fivesome , pentad , quintet , quintuplet |
| 6 | halfdozen , hexad , sextuplet |
| 7 | seven , heptad , septet , septuple , walkingstick |
| 8 | eight , octave , octonary , octuplet , ogdoad |
| 11 | onze , ounze , banker |
| 12 | dozen |
| 13 | longdozen |
Most of the previous losers have at least one winner. 0 and 1 are easy to see why - all blanks gives you 0 points, and most names for 1 have a letter that only has one point.
I’ll just add a function to show where the blank tile(s) are appearing, and I’ll do that table again:
blankify <- function(word, mask) {
word %>%
str_extract_all("[a-z]") %>%
unlist() %>%
replace(which(mask == 0), "☐") %>%
str_flatten()
}
blank_scores %>%
select(Number, sequence, name, score_with_blanks) %>%
filter(Number == score_with_blanks, Number > 0) %>%
mutate(name_with_blanks = blankify(name, sequence)) %>%
select(name, name_with_blanks,Number) %>%
group_by(Number, name) %>%
summarise(name_with_blanks = str_flatten(name_with_blanks, " , ")) %>%
ungroup() %>%
dplyr::arrange(Number) %>%
knitr::kable()| Number | name | name_with_blanks |
|---|---|---|
| 1 | ace | ☐☐e , a☐☐ |
| 1 | individual | ☐☐☐☐☐☐☐☐☐l , ☐☐☐☐☐☐☐☐a☐ , ☐☐☐☐☐☐☐u☐☐ , ☐☐☐☐☐i☐☐☐☐ , ☐☐☐i☐☐☐☐☐☐ , ☐n☐☐☐☐☐☐☐☐ , i☐☐☐☐☐☐☐☐☐ |
| 1 | one | ☐☐e , ☐n☐ , o☐☐ |
| 1 | pratham | ☐☐☐☐☐a☐ , ☐☐☐t☐☐☐ , ☐☐a☐☐☐☐ , ☐r☐☐☐☐☐ |
| 1 | single | ☐☐☐☐☐e , ☐☐☐☐l☐ , ☐☐n☐☐☐ , ☐i☐☐☐☐ , s☐☐☐☐☐ |
| 1 | singleton | ☐☐☐☐☐☐☐☐n , ☐☐☐☐☐☐☐o☐ , ☐☐☐☐☐☐t☐☐ , ☐☐☐☐☐e☐☐☐ , ☐☐☐☐l☐☐☐☐ , ☐☐n☐☐☐☐☐☐ , ☐i☐☐☐☐☐☐☐ , s☐☐☐☐☐☐☐☐ |
| 1 | unary | ☐☐☐r☐ , ☐☐a☐☐ , ☐n☐☐☐ , u☐☐☐☐ |
| 1 | unit | ☐☐☐t , ☐☐i☐ , ☐n☐☐ , u☐☐☐ |
| 1 | unity | ☐☐☐t☐ , ☐☐i☐☐ , ☐n☐☐☐ , u☐☐☐☐ |
| 2 | binary | ☐☐☐ar☐ , ☐☐n☐r☐ , ☐☐na☐☐ , ☐i☐☐r☐ , ☐i☐a☐☐ , ☐in☐☐☐ |
| 2 | brace | ☐☐a☐e , ☐r☐☐e , ☐ra☐☐ |
| 2 | couple | ☐☐☐☐le , ☐☐u☐☐e , ☐☐u☐l☐ , ☐o☐☐☐e , ☐o☐☐l☐ , ☐ou☐☐☐ |
| 2 | couplet | ☐☐☐☐☐et , ☐☐☐☐l☐t , ☐☐☐☐le☐ , ☐☐u☐☐☐t , ☐☐u☐☐e☐ , ☐☐u☐l☐☐ , ☐o☐☐☐☐t , ☐o☐☐☐e☐ , ☐o☐☐l☐☐ , ☐ou☐☐☐☐ |
| 2 | deuce | ☐☐u☐e , ☐e☐☐e , ☐eu☐☐ , d☐☐☐☐ |
| 2 | distich | ☐☐☐ti☐☐ , ☐☐s☐i☐☐ , ☐☐st☐☐☐ , ☐i☐☐i☐☐ , ☐i☐t☐☐☐ , ☐is☐☐☐☐ , d☐☐☐☐☐☐ |
| 2 | double | ☐☐☐☐le , ☐☐u☐☐e , ☐☐u☐l☐ , ☐o☐☐☐e , ☐o☐☐l☐ , ☐ou☐☐☐ , d☐☐☐☐☐ |
| 2 | doubleton | ☐☐☐☐☐☐☐on , ☐☐☐☐☐☐t☐n , ☐☐☐☐☐☐to☐ , ☐☐☐☐☐e☐☐n , ☐☐☐☐☐e☐o☐ , ☐☐☐☐☐et☐☐ , ☐☐☐☐l☐☐☐n , ☐☐☐☐l☐☐o☐ , ☐☐☐☐l☐t☐☐ , ☐☐☐☐le☐☐☐ , ☐☐u☐☐☐☐☐n , ☐☐u☐☐☐☐o☐ , ☐☐u☐☐☐t☐☐ , ☐☐u☐☐e☐☐☐ , ☐☐u☐l☐☐☐☐ , ☐o☐☐☐☐☐☐n , ☐o☐☐☐☐☐o☐ , ☐o☐☐☐☐t☐☐ , ☐o☐☐☐e☐☐☐ , ☐o☐☐l☐☐☐☐ , ☐ou☐☐☐☐☐☐ , d☐☐☐☐☐☐☐☐ |
| 2 | duad | ☐☐☐d , ☐ua☐ , d☐☐☐ |
| 2 | duality | ☐☐☐☐it☐ , ☐☐☐l☐t☐ , ☐☐☐li☐☐ , ☐☐a☐☐t☐ , ☐☐a☐i☐☐ , ☐☐al☐☐☐ , ☐u☐☐☐t☐ , ☐u☐☐i☐☐ , ☐u☐l☐☐☐ , ☐ua☐☐☐☐ , d☐☐☐☐☐☐ |
| 2 | duet | ☐☐et , ☐u☐t , ☐ue☐ , d☐☐☐ |
| 2 | duo | ☐uo , d☐☐ |
| 2 | dyad | ☐☐☐d , d☐☐☐ |
| 2 | pair | ☐☐ir , ☐a☐r , ☐ai☐ |
| 2 | span | ☐☐an , s☐☐n , s☐a☐ |
| 2 | twain | ☐☐☐in , ☐☐a☐n , ☐☐ai☐ , t☐☐☐n , t☐☐i☐ , t☐a☐☐ |
| 2 | twin | ☐☐in , t☐☐n , t☐i☐ |
| 2 | two | t☐o |
| 2 | twosome | ☐☐☐☐o☐e , ☐☐☐s☐☐e , ☐☐☐so☐☐ , ☐☐o☐☐☐e , ☐☐o☐o☐☐ , ☐☐os☐☐☐ , t☐☐☐☐☐e , t☐☐☐o☐☐ , t☐☐s☐☐☐ , t☐o☐☐☐☐ |
| 2 | yoke | ☐o☐e |
| 3 | deuceace | ☐☐☐☐☐☐c☐ , ☐☐☐☐ea☐e , ☐☐☐c☐☐☐☐ , ☐☐u☐☐a☐e , ☐☐u☐e☐☐e , ☐☐u☐ea☐☐ , ☐e☐☐☐a☐e , ☐e☐☐e☐☐e , ☐e☐☐ea☐☐ , ☐eu☐☐☐☐e , ☐eu☐☐a☐☐ , ☐eu☐e☐☐☐ , d☐☐☐☐☐☐e , d☐☐☐☐a☐☐ , d☐☐☐e☐☐☐ , d☐u☐☐☐☐☐ , de☐☐☐☐☐☐ |
| 3 | hattrick | ☐☐☐☐☐☐c☐ , ☐☐☐tri☐☐ , ☐☐t☐ri☐☐ , ☐☐tt☐i☐☐ , ☐☐ttr☐☐☐ , ☐a☐☐ri☐☐ , ☐a☐t☐i☐☐ , ☐a☐tr☐☐☐ , ☐at☐☐i☐☐ , ☐at☐r☐☐☐ , ☐att☐☐☐☐ |
| 3 | leash | ☐eas☐ , l☐as☐ , le☐s☐ , lea☐☐ |
| 3 | tercet | ☐☐☐c☐☐ , ☐☐r☐et , ☐e☐☐et , ☐er☐☐t , ☐er☐e☐ , t☐☐☐et , t☐r☐☐t , t☐r☐e☐ , te☐☐☐t , te☐☐e☐ , ter☐☐☐ |
| 3 | ternary | ☐☐☐nar☐ , ☐☐r☐ar☐ , ☐☐rn☐r☐ , ☐☐rna☐☐ , ☐e☐☐ar☐ , ☐e☐n☐r☐ , ☐e☐na☐☐ , ☐er☐☐r☐ , ☐er☐a☐☐ , ☐ern☐☐☐ , t☐☐☐ar☐ , t☐☐n☐r☐ , t☐☐na☐☐ , t☐r☐☐r☐ , t☐r☐a☐☐ , t☐rn☐☐☐ , te☐☐☐r☐ , te☐☐a☐☐ , te☐n☐☐☐ , ter☐☐☐☐ |
| 3 | ternion | ☐☐☐☐ion , ☐☐☐n☐on , ☐☐☐ni☐n , ☐☐☐nio☐ , ☐☐r☐☐on , ☐☐r☐i☐n , ☐☐r☐io☐ , ☐☐rn☐☐n , ☐☐rn☐o☐ , ☐☐rni☐☐ , ☐e☐☐☐on , ☐e☐☐i☐n , ☐e☐☐io☐ , ☐e☐n☐☐n , ☐e☐n☐o☐ , ☐e☐ni☐☐ , ☐er☐☐☐n , ☐er☐☐o☐ , ☐er☐i☐☐ , ☐ern☐☐☐ , t☐☐☐☐on , t☐☐☐i☐n , t☐☐☐io☐ , t☐☐n☐☐n , t☐☐n☐o☐ , t☐☐ni☐☐ , t☐r☐☐☐n , t☐r☐☐o☐ , t☐r☐i☐☐ , t☐rn☐☐☐ , te☐☐☐☐n , te☐☐☐o☐ , te☐☐i☐☐ , te☐n☐☐☐ , ter☐☐☐☐ |
| 3 | terzetto | ☐☐☐☐☐tto , ☐☐☐☐e☐to , ☐☐☐☐et☐o , ☐☐☐☐ett☐ , ☐☐r☐☐☐to , ☐☐r☐☐t☐o , ☐☐r☐☐tt☐ , ☐☐r☐e☐☐o , ☐☐r☐e☐t☐ , ☐☐r☐et☐☐ , ☐e☐☐☐☐to , ☐e☐☐☐t☐o , ☐e☐☐☐tt☐ , ☐e☐☐e☐☐o , ☐e☐☐e☐t☐ , ☐e☐☐et☐☐ , ☐er☐☐☐☐o , ☐er☐☐☐t☐ , ☐er☐☐t☐☐ , ☐er☐e☐☐☐ , t☐☐☐☐☐to , t☐☐☐☐t☐o , t☐☐☐☐tt☐ , t☐☐☐e☐☐o , t☐☐☐e☐t☐ , t☐☐☐et☐☐ , t☐r☐☐☐☐o , t☐r☐☐☐t☐ , t☐r☐☐t☐☐ , t☐r☐e☐☐☐ , te☐☐☐☐☐o , te☐☐☐☐t☐ , te☐☐☐t☐☐ , te☐☐e☐☐☐ , ter☐☐☐☐☐ |
| 3 | three | ☐☐ree , t☐☐ee , t☐r☐e , t☐re☐ |
| 3 | threesome | ☐☐☐☐☐☐☐m☐ , ☐☐☐☐☐so☐e , ☐☐☐☐e☐o☐e , ☐☐☐☐es☐☐e , ☐☐☐☐eso☐☐ , ☐☐☐e☐☐o☐e , ☐☐☐e☐s☐☐e , ☐☐☐e☐so☐☐ , ☐☐☐ee☐☐☐e , ☐☐☐ee☐o☐☐ , ☐☐☐ees☐☐☐ , ☐☐r☐☐☐o☐e , ☐☐r☐☐s☐☐e , ☐☐r☐☐so☐☐ , ☐☐r☐e☐☐☐e , ☐☐r☐e☐o☐☐ , ☐☐r☐es☐☐☐ , ☐☐re☐☐☐☐e , ☐☐re☐☐o☐☐ , ☐☐re☐s☐☐☐ , ☐☐ree☐☐☐☐ , t☐☐☐☐☐o☐e , t☐☐☐☐s☐☐e , t☐☐☐☐so☐☐ , t☐☐☐e☐☐☐e , t☐☐☐e☐o☐☐ , t☐☐☐es☐☐☐ , t☐☐e☐☐☐☐e , t☐☐e☐☐o☐☐ , t☐☐e☐s☐☐☐ , t☐☐ee☐☐☐☐ , t☐r☐☐☐☐☐e , t☐r☐☐☐o☐☐ , t☐r☐☐s☐☐☐ , t☐r☐e☐☐☐☐ , t☐re☐☐☐☐☐ |
| 3 | tierce | ☐☐☐☐c☐ , ☐☐er☐e , ☐i☐r☐e , ☐ie☐☐e , ☐ier☐☐ , t☐☐r☐e , t☐e☐☐e , t☐er☐☐ , ti☐☐☐e , ti☐r☐☐ , tie☐☐☐ |
| 3 | trey | tre☐ |
| 3 | triad | ☐☐☐ad , ☐☐i☐d , ☐r☐☐d , ☐ria☐ , t☐☐☐d , t☐ia☐ , tr☐a☐ , tri☐☐ |
| 3 | trine | ☐☐ine , ☐r☐ne , ☐ri☐e , ☐rin☐ , t☐☐ne , t☐i☐e , t☐in☐ , tr☐☐e , tr☐n☐ , tri☐☐ |
| 3 | trinity | ☐☐☐nit☐ , ☐☐i☐it☐ , ☐☐in☐t☐ , ☐☐ini☐☐ , ☐r☐☐it☐ , ☐r☐n☐t☐ , ☐r☐ni☐☐ , ☐ri☐☐t☐ , ☐ri☐i☐☐ , ☐rin☐☐☐ , t☐☐☐it☐ , t☐☐n☐t☐ , t☐☐ni☐☐ , t☐i☐☐t☐ , t☐i☐i☐☐ , t☐in☐☐☐ , tr☐☐☐t☐ , tr☐☐i☐☐ , tr☐n☐☐☐ , tri☐☐☐☐ |
| 3 | trio | ☐rio , t☐io , tr☐o , tri☐ |
| 3 | triplet | ☐☐☐☐let , ☐☐☐p☐☐☐ , ☐☐i☐☐et , ☐☐i☐l☐t , ☐☐i☐le☐ , ☐r☐☐☐et , ☐r☐☐l☐t , ☐r☐☐le☐ , ☐ri☐☐☐t , ☐ri☐☐e☐ , ☐ri☐l☐☐ , t☐☐☐☐et , t☐☐☐l☐t , t☐☐☐le☐ , t☐i☐☐☐t , t☐i☐☐e☐ , t☐i☐l☐☐ , tr☐☐☐☐t , tr☐☐☐e☐ , tr☐☐l☐☐ , tri☐☐☐☐ |
| 3 | troika | ☐☐oi☐a , ☐r☐i☐a , ☐ro☐☐a , ☐roi☐☐ , t☐☐i☐a , t☐o☐☐a , t☐oi☐☐ , tr☐☐☐a , tr☐i☐☐ , tro☐☐☐ |
| 4 | four | f☐☐☐ |
| 4 | foursome | ☐☐☐☐☐☐me , ☐☐☐☐☐om☐ , ☐☐☐☐s☐m☐ , ☐☐☐r☐☐m☐ , ☐☐☐rso☐e , ☐☐u☐☐☐m☐ , ☐☐u☐so☐e , ☐☐ur☐o☐e , ☐☐urs☐☐e , ☐☐urso☐☐ , ☐o☐☐☐☐m☐ , ☐o☐☐so☐e , ☐o☐r☐o☐e , ☐o☐rs☐☐e , ☐o☐rso☐☐ , ☐ou☐☐o☐e , ☐ou☐s☐☐e , ☐ou☐so☐☐ , ☐our☐☐☐e , ☐our☐o☐☐ , ☐ours☐☐☐ , f☐☐☐☐☐☐☐ |
| 4 | quadruplet | ☐☐☐☐☐☐p☐☐t , ☐☐☐☐☐☐p☐e☐ , ☐☐☐☐☐☐pl☐☐ , ☐☐☐☐☐u☐let , ☐☐☐☐☐up☐☐☐ , ☐☐☐☐r☐☐let , ☐☐☐☐r☐p☐☐☐ , ☐☐☐☐ru☐☐et , ☐☐☐☐ru☐l☐t , ☐☐☐☐ru☐le☐ , ☐☐☐d☐☐☐☐et , ☐☐☐d☐☐☐l☐t , ☐☐☐d☐☐☐le☐ , ☐☐☐d☐u☐☐☐t , ☐☐☐d☐u☐☐e☐ , ☐☐☐d☐u☐l☐☐ , ☐☐☐dr☐☐☐☐t , ☐☐☐dr☐☐☐e☐ , ☐☐☐dr☐☐l☐☐ , ☐☐☐dru☐☐☐☐ , ☐☐a☐☐☐☐let , ☐☐a☐☐☐p☐☐☐ , ☐☐a☐☐u☐☐et , ☐☐a☐☐u☐l☐t , ☐☐a☐☐u☐le☐ , ☐☐a☐r☐☐☐et , ☐☐a☐r☐☐l☐t , ☐☐a☐r☐☐le☐ , ☐☐a☐ru☐☐☐t , ☐☐a☐ru☐☐e☐ , ☐☐a☐ru☐l☐☐ , ☐☐ad☐☐☐☐☐t , ☐☐ad☐☐☐☐e☐ , ☐☐ad☐☐☐l☐☐ , ☐☐ad☐u☐☐☐☐ , ☐☐adr☐☐☐☐☐ , ☐u☐☐☐☐☐let , ☐u☐☐☐☐p☐☐☐ , ☐u☐☐☐u☐☐et , ☐u☐☐☐u☐l☐t , ☐u☐☐☐u☐le☐ , ☐u☐☐r☐☐☐et , ☐u☐☐r☐☐l☐t , ☐u☐☐r☐☐le☐ , ☐u☐☐ru☐☐☐t , ☐u☐☐ru☐☐e☐ , ☐u☐☐ru☐l☐☐ , ☐u☐d☐☐☐☐☐t , ☐u☐d☐☐☐☐e☐ , ☐u☐d☐☐☐l☐☐ , ☐u☐d☐u☐☐☐☐ , ☐u☐dr☐☐☐☐☐ , ☐ua☐☐☐☐☐et , ☐ua☐☐☐☐l☐t , ☐ua☐☐☐☐le☐ , ☐ua☐☐u☐☐☐t , ☐ua☐☐u☐☐e☐ , ☐ua☐☐u☐l☐☐ , ☐ua☐r☐☐☐☐t , ☐ua☐r☐☐☐e☐ , ☐ua☐r☐☐l☐☐ , ☐ua☐ru☐☐☐☐ , ☐uad☐☐☐☐☐☐ |
| 4 | quartet | ☐☐☐rtet , ☐☐a☐tet , ☐☐ar☐et , ☐☐art☐t , ☐☐arte☐ , ☐u☐☐tet , ☐u☐r☐et , ☐u☐rt☐t , ☐u☐rte☐ , ☐ua☐☐et , ☐ua☐t☐t , ☐ua☐te☐ , ☐uar☐☐t , ☐uar☐e☐ , ☐uart☐☐ |
| 4 | quatern | ☐☐☐tern , ☐☐a☐ern , ☐☐at☐rn , ☐☐ate☐n , ☐☐ater☐ , ☐u☐☐ern , ☐u☐t☐rn , ☐u☐te☐n , ☐u☐ter☐ , ☐ua☐☐rn , ☐ua☐e☐n , ☐ua☐er☐ , ☐uat☐☐n , ☐uat☐r☐ , ☐uate☐☐ |
| 4 | quaternary | ☐☐☐☐☐☐☐☐☐y , ☐☐☐☐☐rnar☐ , ☐☐☐☐e☐nar☐ , ☐☐☐☐er☐ar☐ , ☐☐☐☐ern☐r☐ , ☐☐☐☐erna☐☐ , ☐☐☐t☐☐nar☐ , ☐☐☐t☐r☐ar☐ , ☐☐☐t☐rn☐r☐ , ☐☐☐t☐rna☐☐ , ☐☐☐te☐☐ar☐ , ☐☐☐te☐n☐r☐ , ☐☐☐te☐na☐☐ , ☐☐☐ter☐☐r☐ , ☐☐☐ter☐a☐☐ , ☐☐☐tern☐☐☐ , ☐☐a☐☐☐nar☐ , ☐☐a☐☐r☐ar☐ , ☐☐a☐☐rn☐r☐ , ☐☐a☐☐rna☐☐ , ☐☐a☐e☐☐ar☐ , ☐☐a☐e☐n☐r☐ , ☐☐a☐e☐na☐☐ , ☐☐a☐er☐☐r☐ , ☐☐a☐er☐a☐☐ , ☐☐a☐ern☐☐☐ , ☐☐at☐☐☐ar☐ , ☐☐at☐☐n☐r☐ , ☐☐at☐☐na☐☐ , ☐☐at☐r☐☐r☐ , ☐☐at☐r☐a☐☐ , ☐☐at☐rn☐☐☐ , ☐☐ate☐☐☐r☐ , ☐☐ate☐☐a☐☐ , ☐☐ate☐n☐☐☐ , ☐☐ater☐☐☐☐ , ☐u☐☐☐☐nar☐ , ☐u☐☐☐r☐ar☐ , ☐u☐☐☐rn☐r☐ , ☐u☐☐☐rna☐☐ , ☐u☐☐e☐☐ar☐ , ☐u☐☐e☐n☐r☐ , ☐u☐☐e☐na☐☐ , ☐u☐☐er☐☐r☐ , ☐u☐☐er☐a☐☐ , ☐u☐☐ern☐☐☐ , ☐u☐t☐☐☐ar☐ , ☐u☐t☐☐n☐r☐ , ☐u☐t☐☐na☐☐ , ☐u☐t☐r☐☐r☐ , ☐u☐t☐r☐a☐☐ , ☐u☐t☐rn☐☐☐ , ☐u☐te☐☐☐r☐ , ☐u☐te☐☐a☐☐ , ☐u☐te☐n☐☐☐ , ☐u☐ter☐☐☐☐ , ☐ua☐☐☐☐ar☐ , ☐ua☐☐☐n☐r☐ , ☐ua☐☐☐na☐☐ , ☐ua☐☐r☐☐r☐ , ☐ua☐☐r☐a☐☐ , ☐ua☐☐rn☐☐☐ , ☐ua☐e☐☐☐r☐ , ☐ua☐e☐☐a☐☐ , ☐ua☐e☐n☐☐☐ , ☐ua☐er☐☐☐☐ , ☐uat☐☐☐☐r☐ , ☐uat☐☐☐a☐☐ , ☐uat☐☐n☐☐☐ , ☐uat☐r☐☐☐☐ , ☐uate☐☐☐☐☐ |
| 4 | quaternity | ☐☐☐☐☐☐☐☐☐y , ☐☐☐☐☐rnit☐ , ☐☐☐☐e☐nit☐ , ☐☐☐☐er☐it☐ , ☐☐☐☐ern☐t☐ , ☐☐☐☐erni☐☐ , ☐☐☐t☐☐nit☐ , ☐☐☐t☐r☐it☐ , ☐☐☐t☐rn☐t☐ , ☐☐☐t☐rni☐☐ , ☐☐☐te☐☐it☐ , ☐☐☐te☐n☐t☐ , ☐☐☐te☐ni☐☐ , ☐☐☐ter☐☐t☐ , ☐☐☐ter☐i☐☐ , ☐☐☐tern☐☐☐ , ☐☐a☐☐☐nit☐ , ☐☐a☐☐r☐it☐ , ☐☐a☐☐rn☐t☐ , ☐☐a☐☐rni☐☐ , ☐☐a☐e☐☐it☐ , ☐☐a☐e☐n☐t☐ , ☐☐a☐e☐ni☐☐ , ☐☐a☐er☐☐t☐ , ☐☐a☐er☐i☐☐ , ☐☐a☐ern☐☐☐ , ☐☐at☐☐☐it☐ , ☐☐at☐☐n☐t☐ , ☐☐at☐☐ni☐☐ , ☐☐at☐r☐☐t☐ , ☐☐at☐r☐i☐☐ , ☐☐at☐rn☐☐☐ , ☐☐ate☐☐☐t☐ , ☐☐ate☐☐i☐☐ , ☐☐ate☐n☐☐☐ , ☐☐ater☐☐☐☐ , ☐u☐☐☐☐nit☐ , ☐u☐☐☐r☐it☐ , ☐u☐☐☐rn☐t☐ , ☐u☐☐☐rni☐☐ , ☐u☐☐e☐☐it☐ , ☐u☐☐e☐n☐t☐ , ☐u☐☐e☐ni☐☐ , ☐u☐☐er☐☐t☐ , ☐u☐☐er☐i☐☐ , ☐u☐☐ern☐☐☐ , ☐u☐t☐☐☐it☐ , ☐u☐t☐☐n☐t☐ , ☐u☐t☐☐ni☐☐ , ☐u☐t☐r☐☐t☐ , ☐u☐t☐r☐i☐☐ , ☐u☐t☐rn☐☐☐ , ☐u☐te☐☐☐t☐ , ☐u☐te☐☐i☐☐ , ☐u☐te☐n☐☐☐ , ☐u☐ter☐☐☐☐ , ☐ua☐☐☐☐it☐ , ☐ua☐☐☐n☐t☐ , ☐ua☐☐☐ni☐☐ , ☐ua☐☐r☐☐t☐ , ☐ua☐☐r☐i☐☐ , ☐ua☐☐rn☐☐☐ , ☐ua☐e☐☐☐t☐ , ☐ua☐e☐☐i☐☐ , ☐ua☐e☐n☐☐☐ , ☐ua☐er☐☐☐☐ , ☐uat☐☐☐☐t☐ , ☐uat☐☐☐i☐☐ , ☐uat☐☐n☐☐☐ , ☐uat☐r☐☐☐☐ , ☐uate☐☐☐☐☐ |
| 4 | tetrad | ☐☐☐rad , ☐☐t☐ad , ☐☐tr☐d , ☐e☐☐ad , ☐e☐r☐d , ☐et☐☐d , ☐etra☐ , t☐☐☐ad , t☐☐r☐d , t☐t☐☐d , t☐tra☐ , te☐☐☐d , te☐ra☐ , tet☐a☐ , tetr☐☐ |
| 5 | cinque | c☐☐☐ue , c☐n☐☐e , c☐n☐u☐ , ci☐☐☐e , ci☐☐u☐ , cin☐☐☐ |
| 5 | fin | f☐n , fi☐ |
| 5 | five | ☐☐ve , ☐iv☐ , f☐☐e , fi☐☐ |
| 5 | fivesome | ☐☐☐☐☐ome , ☐☐☐☐s☐me , ☐☐☐☐som☐ , ☐☐☐e☐☐me , ☐☐☐e☐om☐ , ☐☐☐es☐m☐ , ☐☐v☐☐☐☐e , ☐☐v☐☐o☐☐ , ☐☐v☐s☐☐☐ , ☐☐ve☐☐☐☐ , ☐i☐☐☐☐me , ☐i☐☐☐om☐ , ☐i☐☐s☐m☐ , ☐i☐e☐☐m☐ , ☐i☐eso☐e , ☐iv☐☐☐☐☐ , f☐☐☐☐☐☐e , f☐☐☐☐o☐☐ , f☐☐☐s☐☐☐ , f☐☐e☐☐☐☐ , fi☐☐☐☐☐☐ |
| 5 | pentad | ☐☐ntad , ☐e☐tad , ☐en☐ad , ☐ent☐d , p☐☐☐☐d , p☐☐ta☐ , p☐n☐a☐ , p☐nt☐☐ , pe☐☐a☐ , pe☐t☐☐ , pen☐☐☐ |
| 5 | quintet | ☐☐intet , ☐u☐ntet , ☐ui☐tet , ☐uin☐et , ☐uint☐t , ☐uinte☐ |
| 5 | quintuplet | ☐☐☐☐☐☐p☐et , ☐☐☐☐☐☐pl☐t , ☐☐☐☐☐☐ple☐ , ☐☐☐☐☐up☐☐t , ☐☐☐☐☐up☐e☐ , ☐☐☐☐☐upl☐☐ , ☐☐☐☐t☐p☐☐t , ☐☐☐☐t☐p☐e☐ , ☐☐☐☐t☐pl☐☐ , ☐☐☐☐tu☐let , ☐☐☐☐tup☐☐☐ , ☐☐☐n☐☐p☐☐t , ☐☐☐n☐☐p☐e☐ , ☐☐☐n☐☐pl☐☐ , ☐☐☐n☐u☐let , ☐☐☐n☐up☐☐☐ , ☐☐☐nt☐☐let , ☐☐☐nt☐p☐☐☐ , ☐☐☐ntu☐☐et , ☐☐☐ntu☐l☐t , ☐☐☐ntu☐le☐ , ☐☐i☐☐☐p☐☐t , ☐☐i☐☐☐p☐e☐ , ☐☐i☐☐☐pl☐☐ , ☐☐i☐☐u☐let , ☐☐i☐☐up☐☐☐ , ☐☐i☐t☐☐let , ☐☐i☐t☐p☐☐☐ , ☐☐i☐tu☐☐et , ☐☐i☐tu☐l☐t , ☐☐i☐tu☐le☐ , ☐☐in☐☐☐let , ☐☐in☐☐p☐☐☐ , ☐☐in☐u☐☐et , ☐☐in☐u☐l☐t , ☐☐in☐u☐le☐ , ☐☐int☐☐☐et , ☐☐int☐☐l☐t , ☐☐int☐☐le☐ , ☐☐intu☐☐☐t , ☐☐intu☐☐e☐ , ☐☐intu☐l☐☐ , ☐u☐☐☐☐p☐☐t , ☐u☐☐☐☐p☐e☐ , ☐u☐☐☐☐pl☐☐ , ☐u☐☐☐u☐let , ☐u☐☐☐up☐☐☐ , ☐u☐☐t☐☐let , ☐u☐☐t☐p☐☐☐ , ☐u☐☐tu☐☐et , ☐u☐☐tu☐l☐t , ☐u☐☐tu☐le☐ , ☐u☐n☐☐☐let , ☐u☐n☐☐p☐☐☐ , ☐u☐n☐u☐☐et , ☐u☐n☐u☐l☐t , ☐u☐n☐u☐le☐ , ☐u☐nt☐☐☐et , ☐u☐nt☐☐l☐t , ☐u☐nt☐☐le☐ , ☐u☐ntu☐☐☐t , ☐u☐ntu☐☐e☐ , ☐u☐ntu☐l☐☐ , ☐ui☐☐☐☐let , ☐ui☐☐☐p☐☐☐ , ☐ui☐☐u☐☐et , ☐ui☐☐u☐l☐t , ☐ui☐☐u☐le☐ , ☐ui☐t☐☐☐et , ☐ui☐t☐☐l☐t , ☐ui☐t☐☐le☐ , ☐ui☐tu☐☐☐t , ☐ui☐tu☐☐e☐ , ☐ui☐tu☐l☐☐ , ☐uin☐☐☐☐et , ☐uin☐☐☐l☐t , ☐uin☐☐☐le☐ , ☐uin☐u☐☐☐t , ☐uin☐u☐☐e☐ , ☐uin☐u☐l☐☐ , ☐uint☐☐☐☐t , ☐uint☐☐☐e☐ , ☐uint☐☐l☐☐ , ☐uintu☐☐☐☐ |
| 6 | halfdozen | ☐☐☐f☐☐☐en , ☐☐☐f☐o☐☐n , ☐☐☐f☐o☐e☐ , ☐☐☐fd☐☐☐☐ , ☐☐l☐do☐en , ☐☐lf☐☐☐☐n , ☐☐lf☐☐☐e☐ , ☐☐lf☐o☐☐☐ , ☐a☐☐do☐en , ☐a☐f☐☐☐☐n , ☐a☐f☐☐☐e☐ , ☐a☐f☐o☐☐☐ , ☐al☐d☐☐en , ☐al☐do☐☐n , ☐al☐do☐e☐ , ☐alf☐☐☐☐☐ , h☐☐☐☐☐☐en , h☐☐☐☐o☐☐n , h☐☐☐☐o☐e☐ , h☐☐☐d☐☐☐☐ , h☐l☐☐☐☐☐n , h☐l☐☐☐☐e☐ , h☐l☐☐o☐☐☐ , ha☐☐☐☐☐☐n , ha☐☐☐☐☐e☐ , ha☐☐☐o☐☐☐ , hal☐☐☐☐☐☐ |
| 6 | hexad | h☐☐☐d , he☐a☐ |
| 6 | sextuplet | ☐☐☐☐☐plet , ☐☐☐☐up☐et , ☐☐☐☐upl☐t , ☐☐☐☐uple☐ , ☐☐☐t☐p☐et , ☐☐☐t☐pl☐t , ☐☐☐t☐ple☐ , ☐☐☐tup☐☐t , ☐☐☐tup☐e☐ , ☐☐☐tupl☐☐ , ☐e☐☐☐p☐et , ☐e☐☐☐pl☐t , ☐e☐☐☐ple☐ , ☐e☐☐up☐☐t , ☐e☐☐up☐e☐ , ☐e☐☐upl☐☐ , ☐e☐t☐p☐☐t , ☐e☐t☐p☐e☐ , ☐e☐t☐pl☐☐ , ☐e☐tu☐let , ☐e☐tup☐☐☐ , s☐☐☐☐p☐et , s☐☐☐☐pl☐t , s☐☐☐☐ple☐ , s☐☐☐up☐☐t , s☐☐☐up☐e☐ , s☐☐☐upl☐☐ , s☐☐t☐p☐☐t , s☐☐t☐p☐e☐ , s☐☐t☐pl☐☐ , s☐☐tu☐let , s☐☐tup☐☐☐ , se☐☐☐p☐☐t , se☐☐☐p☐e☐ , se☐☐☐pl☐☐ , se☐☐u☐let , se☐☐up☐☐☐ , se☐t☐☐let , se☐t☐p☐☐☐ , se☐tu☐☐et , se☐tu☐l☐t , se☐tu☐le☐ |
| 7 | heptad | ☐☐ptad , ☐ep☐ad , ☐ept☐d , h☐☐☐ad , h☐☐t☐d , h☐p☐☐☐ , he☐☐☐d , he☐ta☐ |
| 7 | septet | ☐eptet , s☐ptet , sep☐et , sept☐t , septe☐ |
| 7 | septuple | ☐☐☐tuple , ☐☐p☐☐p☐e , ☐☐p☐☐pl☐ , ☐☐p☐up☐☐ , ☐☐pt☐p☐☐ , ☐☐ptu☐le , ☐e☐☐uple , ☐e☐t☐ple , ☐e☐tup☐e , ☐e☐tupl☐ , ☐ep☐☐p☐☐ , ☐ep☐u☐le , ☐ept☐☐le , ☐eptu☐☐e , ☐eptu☐l☐ , s☐☐☐uple , s☐☐t☐ple , s☐☐tup☐e , s☐☐tupl☐ , s☐p☐☐p☐☐ , s☐p☐u☐le , s☐pt☐☐le , s☐ptu☐☐e , s☐ptu☐l☐ , se☐☐☐ple , se☐☐up☐e , se☐☐upl☐ , se☐t☐p☐e , se☐t☐pl☐ , se☐tup☐☐ , sep☐☐☐le , sep☐u☐☐e , sep☐u☐l☐ , sept☐☐☐e , sept☐☐l☐ , septu☐☐☐ |
| 7 | seven | ☐even , s☐ven , sev☐n , seve☐ |
| 7 | walkingstick | ☐☐☐☐☐☐☐☐ti☐k , ☐☐☐☐☐☐☐s☐i☐k , ☐☐☐☐☐☐☐st☐☐k , ☐☐☐☐☐☐g☐☐☐☐k , ☐☐☐☐☐☐g☐tic☐ , ☐☐☐☐☐☐gs☐ic☐ , ☐☐☐☐☐☐gst☐c☐ , ☐☐☐☐☐n☐☐☐i☐k , ☐☐☐☐☐n☐☐t☐☐k , ☐☐☐☐☐n☐s☐☐☐k , ☐☐☐☐☐n☐stic☐ , ☐☐☐☐☐ng☐☐ic☐ , ☐☐☐☐☐ng☐t☐c☐ , ☐☐☐☐☐ngs☐☐c☐ , ☐☐☐☐i☐☐☐☐i☐k , ☐☐☐☐i☐☐☐t☐☐k , ☐☐☐☐i☐☐s☐☐☐k , ☐☐☐☐i☐☐stic☐ , ☐☐☐☐i☐g☐☐ic☐ , ☐☐☐☐i☐g☐t☐c☐ , ☐☐☐☐i☐gs☐☐c☐ , ☐☐☐☐in☐☐☐☐☐k , ☐☐☐☐in☐☐tic☐ , ☐☐☐☐in☐s☐ic☐ , ☐☐☐☐in☐st☐c☐ , ☐☐☐☐ing☐☐☐c☐ , ☐☐☐☐ingsti☐☐ , ☐☐☐k☐☐☐☐ti☐☐ , ☐☐☐k☐☐☐s☐i☐☐ , ☐☐☐k☐☐☐st☐☐☐ , ☐☐☐k☐☐g☐☐☐☐☐ , ☐☐☐k☐n☐☐☐i☐☐ , ☐☐☐k☐n☐☐t☐☐☐ , ☐☐☐k☐n☐s☐☐☐☐ , ☐☐☐ki☐☐☐☐i☐☐ , ☐☐☐ki☐☐☐t☐☐☐ , ☐☐☐ki☐☐s☐☐☐☐ , ☐☐☐kin☐☐☐☐☐☐ , ☐☐l☐☐☐☐☐☐i☐k , ☐☐l☐☐☐☐☐t☐☐k , ☐☐l☐☐☐☐s☐☐☐k , ☐☐l☐☐☐☐stic☐ , ☐☐l☐☐☐g☐☐ic☐ , ☐☐l☐☐☐g☐t☐c☐ , ☐☐l☐☐☐gs☐☐c☐ , ☐☐l☐☐n☐☐☐☐☐k , ☐☐l☐☐n☐☐tic☐ , ☐☐l☐☐n☐s☐ic☐ , ☐☐l☐☐n☐st☐c☐ , ☐☐l☐☐ng☐☐☐c☐ , ☐☐l☐☐ngsti☐☐ , ☐☐l☐i☐☐☐☐☐☐k , ☐☐l☐i☐☐☐tic☐ , ☐☐l☐i☐☐s☐ic☐ , ☐☐l☐i☐☐st☐c☐ , ☐☐l☐i☐g☐☐☐c☐ , ☐☐l☐i☐gsti☐☐ , ☐☐l☐in☐☐☐ic☐ , ☐☐l☐in☐☐t☐c☐ , ☐☐l☐in☐s☐☐c☐ , ☐☐l☐ing☐ti☐☐ , ☐☐l☐ings☐i☐☐ , ☐☐l☐ingst☐☐☐ , ☐☐lk☐☐☐☐☐i☐☐ , ☐☐lk☐☐☐☐t☐☐☐ , ☐☐lk☐☐☐s☐☐☐☐ , ☐☐lk☐n☐☐☐☐☐☐ , ☐☐lki☐☐☐☐☐☐☐ , ☐a☐☐☐☐☐☐☐i☐k , ☐a☐☐☐☐☐☐t☐☐k , ☐a☐☐☐☐☐s☐☐☐k , ☐a☐☐☐☐☐stic☐ , ☐a☐☐☐☐g☐☐ic☐ , ☐a☐☐☐☐g☐t☐c☐ , ☐a☐☐☐☐gs☐☐c☐ , ☐a☐☐☐n☐☐☐☐☐k , ☐a☐☐☐n☐☐tic☐ , ☐a☐☐☐n☐s☐ic☐ , ☐a☐☐☐n☐st☐c☐ , ☐a☐☐☐ng☐☐☐c☐ , ☐a☐☐☐ngsti☐☐ , ☐a☐☐i☐☐☐☐☐☐k , ☐a☐☐i☐☐☐tic☐ , ☐a☐☐i☐☐s☐ic☐ , ☐a☐☐i☐☐st☐c☐ , ☐a☐☐i☐g☐☐☐c☐ , ☐a☐☐i☐gsti☐☐ , ☐a☐☐in☐☐☐ic☐ , ☐a☐☐in☐☐t☐c☐ , ☐a☐☐in☐s☐☐c☐ , ☐a☐☐ing☐ti☐☐ , ☐a☐☐ings☐i☐☐ , ☐a☐☐ingst☐☐☐ , ☐a☐k☐☐☐☐☐i☐☐ , ☐a☐k☐☐☐☐t☐☐☐ , ☐a☐k☐☐☐s☐☐☐☐ , ☐a☐k☐n☐☐☐☐☐☐ , ☐a☐ki☐☐☐☐☐☐☐ , ☐al☐☐☐☐☐☐☐☐k , ☐al☐☐☐☐☐tic☐ , ☐al☐☐☐☐s☐ic☐ , ☐al☐☐☐☐st☐c☐ , ☐al☐☐☐g☐☐☐c☐ , ☐al☐☐☐gsti☐☐ , ☐al☐☐n☐☐☐ic☐ , ☐al☐☐n☐☐t☐c☐ , ☐al☐☐n☐s☐☐c☐ , ☐al☐☐ng☐ti☐☐ , ☐al☐☐ngs☐i☐☐ , ☐al☐☐ngst☐☐☐ , ☐al☐i☐☐☐☐ic☐ , ☐al☐i☐☐☐t☐c☐ , ☐al☐i☐☐s☐☐c☐ , ☐al☐i☐g☐ti☐☐ , ☐al☐i☐gs☐i☐☐ , ☐al☐i☐gst☐☐☐ , ☐al☐in☐☐☐☐c☐ , ☐al☐in☐sti☐☐ , ☐al☐ing☐☐i☐☐ , ☐al☐ing☐t☐☐☐ , ☐al☐ings☐☐☐☐ , ☐alk☐☐☐☐☐☐☐☐ , w☐☐☐☐☐☐☐☐☐c☐ , w☐☐☐☐☐☐sti☐☐ , w☐☐☐☐☐g☐☐i☐☐ , w☐☐☐☐☐g☐t☐☐☐ , w☐☐☐☐☐gs☐☐☐☐ , w☐☐☐☐n☐☐ti☐☐ , w☐☐☐☐n☐s☐i☐☐ , w☐☐☐☐n☐st☐☐☐ , w☐☐☐☐ng☐☐☐☐☐ , w☐☐☐i☐☐☐ti☐☐ , w☐☐☐i☐☐s☐i☐☐ , w☐☐☐i☐☐st☐☐☐ , w☐☐☐i☐g☐☐☐☐☐ , w☐☐☐in☐☐☐i☐☐ , w☐☐☐in☐☐t☐☐☐ , w☐☐☐in☐s☐☐☐☐ , w☐l☐☐☐☐☐ti☐☐ , w☐l☐☐☐☐s☐i☐☐ , w☐l☐☐☐☐st☐☐☐ , w☐l☐☐☐g☐☐☐☐☐ , w☐l☐☐n☐☐☐i☐☐ , w☐l☐☐n☐☐t☐☐☐ , w☐l☐☐n☐s☐☐☐☐ , w☐l☐i☐☐☐☐i☐☐ , w☐l☐i☐☐☐t☐☐☐ , w☐l☐i☐☐s☐☐☐☐ , w☐l☐in☐☐☐☐☐☐ , wa☐☐☐☐☐☐ti☐☐ , wa☐☐☐☐☐s☐i☐☐ , wa☐☐☐☐☐st☐☐☐ , wa☐☐☐☐g☐☐☐☐☐ , wa☐☐☐n☐☐☐i☐☐ , wa☐☐☐n☐☐t☐☐☐ , wa☐☐☐n☐s☐☐☐☐ , wa☐☐i☐☐☐☐i☐☐ , wa☐☐i☐☐☐t☐☐☐ , wa☐☐i☐☐s☐☐☐☐ , wa☐☐in☐☐☐☐☐☐ , wal☐☐☐☐☐☐i☐☐ , wal☐☐☐☐☐t☐☐☐ , wal☐☐☐☐s☐☐☐☐ , wal☐☐n☐☐☐☐☐☐ , wal☐i☐☐☐☐☐☐☐ |
| 8 | eight | ☐ight , e☐ght , eigh☐ |
| 8 | octave | ☐c☐☐ve , ☐c☐av☐ , ☐ct☐v☐ , o☐tave , oc☐☐v☐ |
| 8 | octonary | ☐☐☐onary , ☐☐t☐nary , ☐☐to☐ary , ☐☐ton☐ry , ☐☐tona☐y , ☐c☐☐☐☐ry , ☐c☐☐☐a☐y , ☐c☐☐n☐☐y , ☐c☐o☐☐☐y , ☐ct☐☐☐☐y , ☐ctonar☐ , o☐☐☐nary , o☐☐o☐ary , o☐☐on☐ry , o☐☐ona☐y , o☐t☐☐ary , o☐t☐n☐ry , o☐t☐na☐y , o☐to☐☐ry , o☐to☐a☐y , o☐ton☐☐y , oc☐☐☐☐☐y , oc☐onar☐ , oct☐nar☐ , octo☐ar☐ , octon☐r☐ , octona☐☐ |
| 8 | octuplet | ☐☐tuplet , ☐c☐☐p☐et , ☐c☐☐pl☐t , ☐c☐☐ple☐ , ☐c☐up☐☐t , ☐c☐up☐e☐ , ☐c☐upl☐☐ , ☐ct☐p☐☐t , ☐ct☐p☐e☐ , ☐ct☐pl☐☐ , ☐ctu☐let , ☐ctup☐☐☐ , o☐☐uplet , o☐t☐plet , o☐tup☐et , o☐tupl☐t , o☐tuple☐ , oc☐☐p☐☐t , oc☐☐p☐e☐ , oc☐☐pl☐☐ , oc☐u☐let , oc☐up☐☐☐ , oct☐☐let , oct☐p☐☐☐ , octu☐☐et , octu☐l☐t , octu☐le☐ |
| 8 | ogdoad | ☐gdoad , ogd☐ad , ogdo☐d |
| 11 | banker | b☐nker , ba☐ker , bank☐r , banke☐ |
| 11 | onze | ☐☐ze , ☐nz☐ , o☐z☐ |
| 11 | ounze | ☐☐☐ze , ☐☐nz☐ , ☐u☐z☐ , o☐☐z☐ |
| 12 | dozen | ☐☐zen , ☐oz☐n , ☐oze☐ , d☐z☐☐ |
| 13 | longdozen | ☐☐☐☐☐ozen , ☐☐☐☐d☐z☐n , ☐☐☐☐d☐ze☐ , ☐☐☐☐doz☐☐ , ☐☐☐g☐☐z☐n , ☐☐☐g☐☐ze☐ , ☐☐☐g☐oz☐☐ , ☐☐n☐☐☐zen , ☐☐n☐☐oz☐n , ☐☐n☐☐oze☐ , ☐☐n☐d☐z☐☐ , ☐☐ng☐☐z☐☐ , ☐o☐☐☐☐zen , ☐o☐☐☐oz☐n , ☐o☐☐☐oze☐ , ☐o☐☐d☐z☐☐ , ☐o☐g☐☐z☐☐ , ☐on☐☐☐z☐n , ☐on☐☐☐ze☐ , ☐on☐☐oz☐☐ , l☐☐☐☐☐zen , l☐☐☐☐oz☐n , l☐☐☐☐oze☐ , l☐☐☐d☐z☐☐ , l☐☐g☐☐z☐☐ , l☐n☐☐☐z☐n , l☐n☐☐☐ze☐ , l☐n☐☐oz☐☐ , lo☐☐☐☐z☐n , lo☐☐☐☐ze☐ , lo☐☐☐oz☐☐ , lon☐☐☐z☐☐ |
Moving on
This suggests a method that can be extended for dealing with double/triple letters, and even triple words, but I feel this post is long enough for now.