Two things are guaranteed to grab my attention in a Riddler Column - Dungeons and Dragons (DnD) and probability spaces small enough to enumerate all combinations.
The default position is roll 1 20-sided die (d20), and the other scenarios involve 4 d20 rolls, with a probability space of 20^4= 160,000. More than I’m willing to do by hand, but R laughs at how easy this is.
die <- 1:20
all_combinations <- list(die_1 = die,die_2=die,die_3=die,die_4=die) %>%
cross_df()result_table <- all_combinations %>%
mutate(advantage_1 = pmax(die_1,die_2), advantage_2 = pmax(die_3,die_4),
dis_1 = pmin(die_1,die_2), dis_2=pmin(die_3,die_4)) %>%
mutate(dis_of_advantage = pmin(advantage_1, advantage_2),
advantage_of_dis = pmax(dis_1,dis_2)) Then the average for each is:
result_table %>%
summarise(default = mean(die_1),
dis_of_advantage = mean(dis_of_advantage),
advantage_of_dis = mean(advantage_of_dis)) %>%
knitr::kable()| default | dis_of_advantage | advantage_of_dis |
|---|---|---|
| 10.5 | 11.16666 | 9.833338 |
So disadvantage of advantage is better than default, which is better than advantage of disadvantage. On average.
The probability of getting exactly each roll is:
result_table %>%
select(die_1, dis_of_advantage, advantage_of_dis) %>%
pivot_longer(1:3) %>%
count(name,value) %>%
group_by(name) %>%
mutate(p=n/sum(n)) %>%
ungroup() %>%
ggplot(aes(x=value,y=p,colour=name)) + geom_line() +
scale_y_continuous(labels=scales::percent) +
expand_limits(y=0) +
theme_minimal()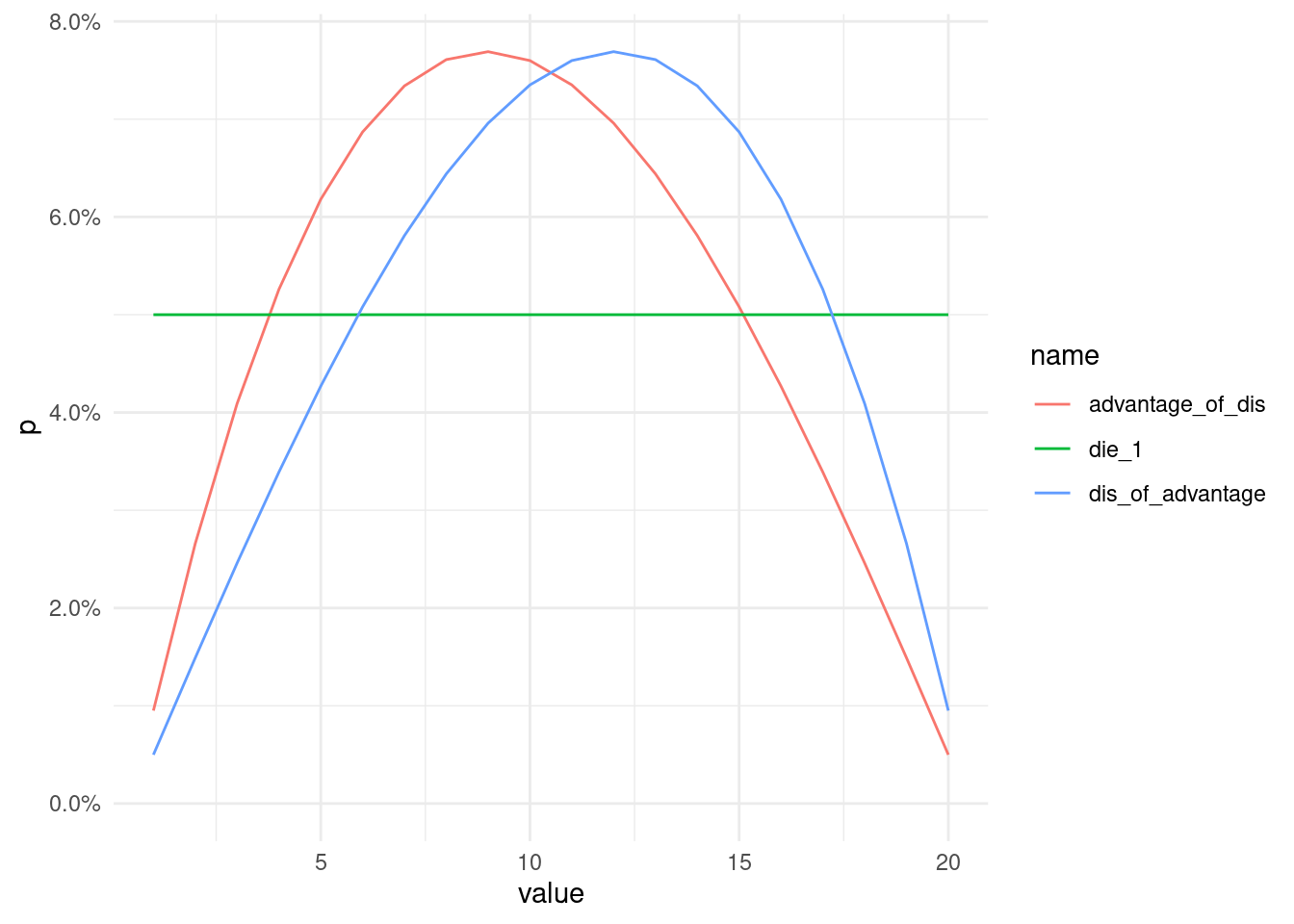
Or the probability of getting at least N on the roll is:
result_table %>%
select(die_1, dis_of_advantage, advantage_of_dis) %>%
pivot_longer(1:3) %>%
count(name,value) %>%
group_by(name) %>%
mutate(p=n/sum(n)) %>%
arrange(-value) %>%
mutate(p=cumsum(p)) %>%
ungroup() %>%
plot_ly(x=~value,y=~p,split=~name) %>%
add_lines() %>%
layout(yaxis = list(tickformat = "%"))