A chaos game

The Sierpinski Triangle is cool, and another blog gave a construction of it as a chaos game.

The other games look very do-able, let’s have a play.

Generally we need to start with a regular n-gon in the plane. Might as well make a function via the parameterisation of the circle as \(\sin(\theta),\cos(\theta)\).

Scrap that, this whole thing works better in Complex arithmetic.

plot_complex_points  <- function(z){
  tibble(Re=Re(z),Im=Im(z)) %>%
    ggplot(aes(x=Re,y=Im)) + scale + theme + geom_point(shape = ".") + coord_equal()
}

poly <- function(n){ #n roots of unity
  complex(modulus = 1, argument = seq(0, 2*pi, length.out = n+1))[-1] #removing the first element to stop double-counting 1+0i.
}

poly(5) %>%
  plot_complex_points()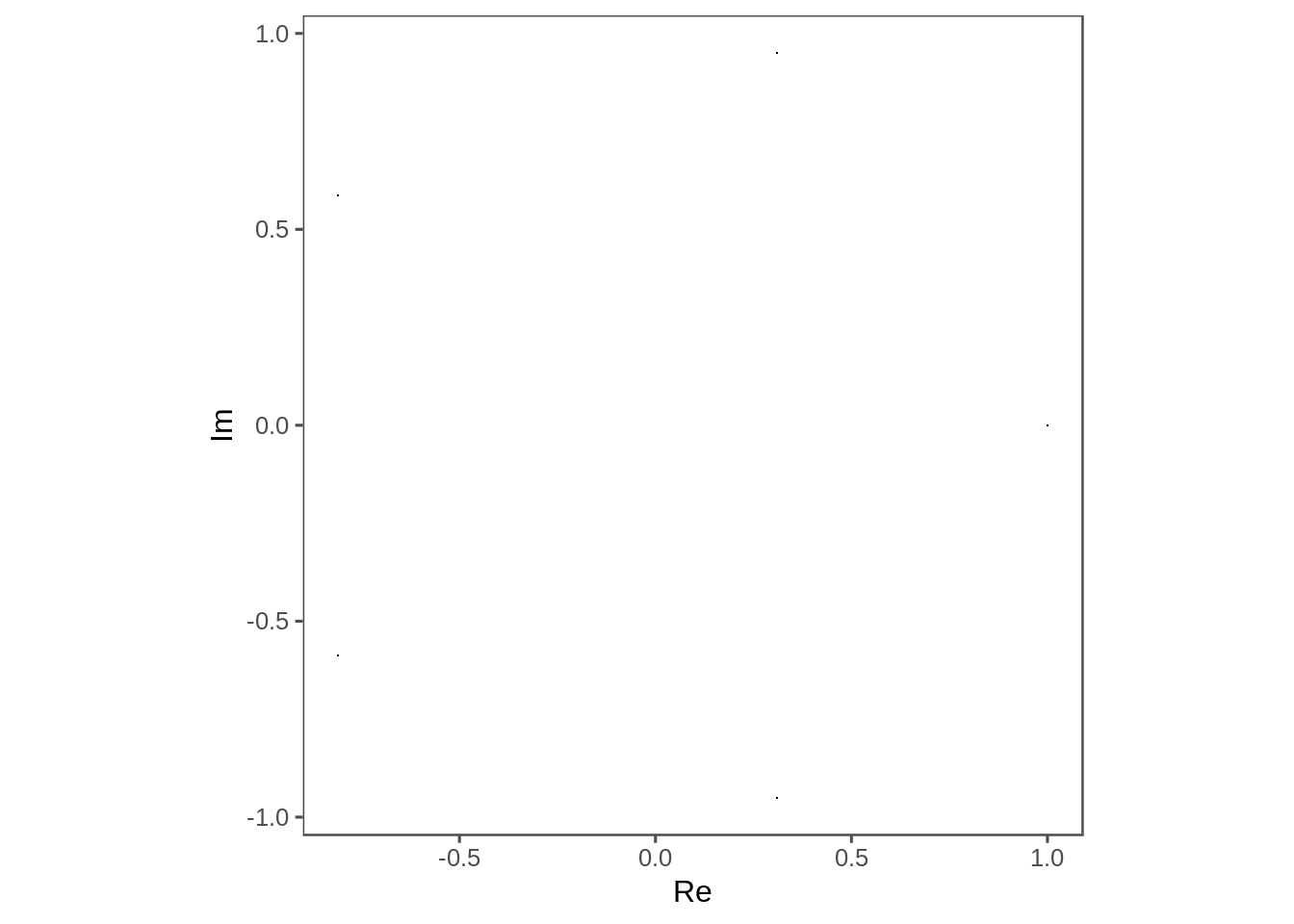

I like the look of rule:

A point inside a pentagon repeatedly jumps half of the distance towards a randomly chosen vertex, but the currently chosen vertex cannot be the same as the previously chosen vertex.

‘Half the distance to’, in the complex plane, is just taking the average. This is nice.

Not choosing the same vertex 2ce is just as simple of numbering the other vertices 1:4.

number_of_points <- 1e6

pentagon <- poly(5)

points <- rep(0i, number_of_points) #slightly better than always extending the lists.

chosen_vertex <- sample(0:3, number_of_points, replace = T)

for(i in 2:number_of_points){

  
  chosen_vertex[i] <- ((chosen_vertex[i-1] + chosen_vertex[i]) %% 5) + 1
  
  this_vertex <- pentagon[chosen_vertex[i]]
  
  points[i] <- (points[i-1] + this_vertex)/2
}


plot_complex_points(points[2:1e4])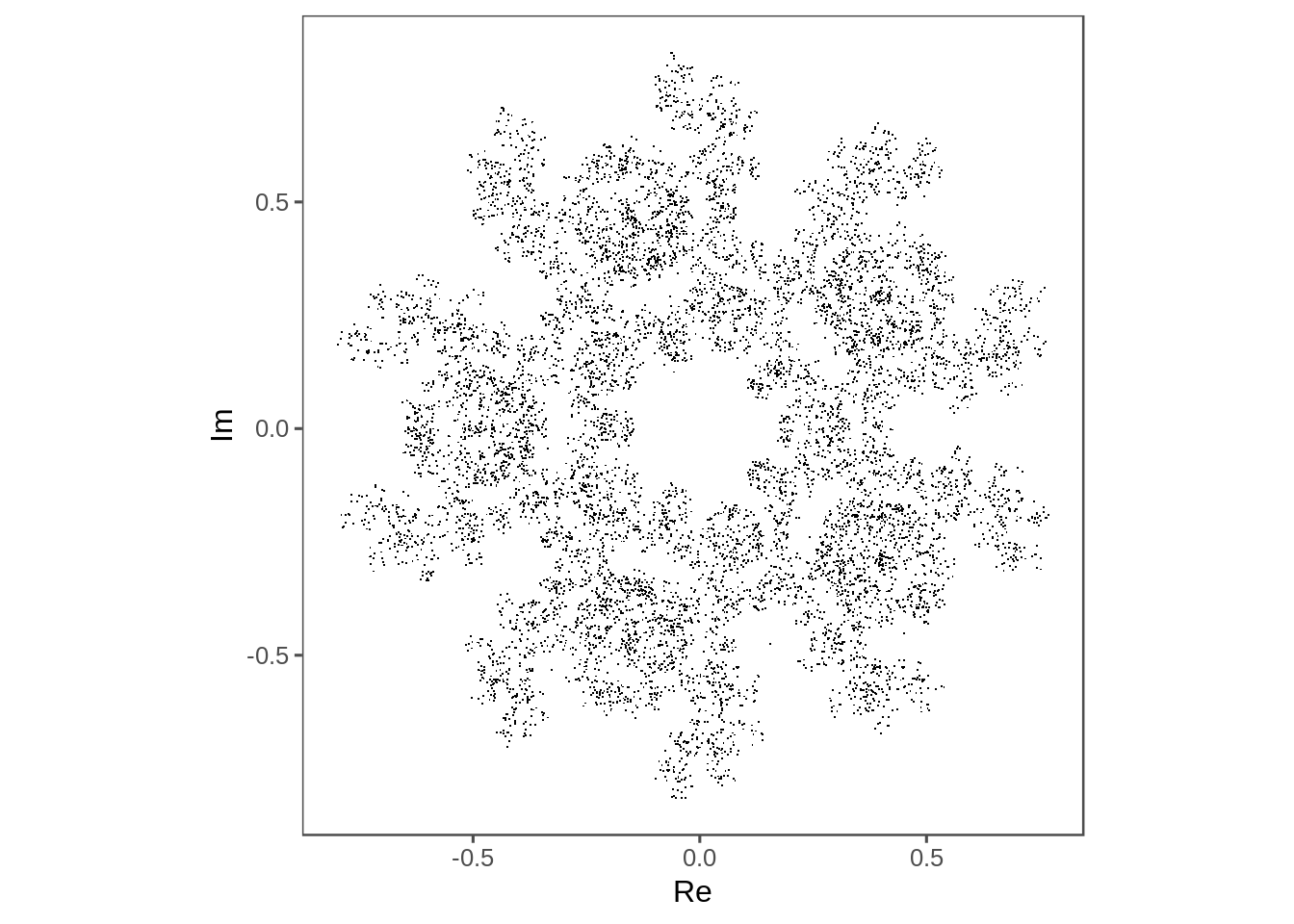

plot_complex_points(points[2:1e5])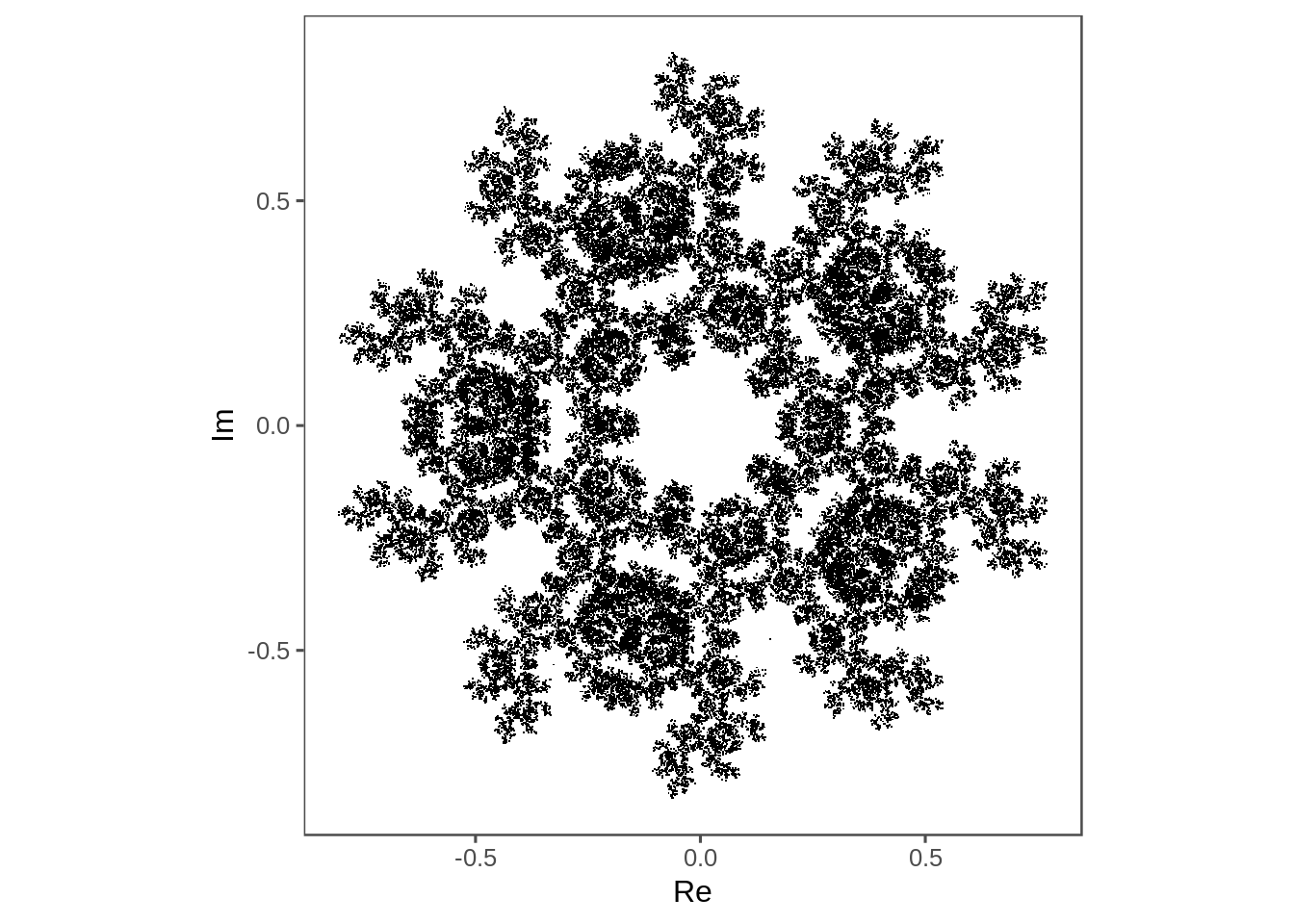

plot_complex_points(points)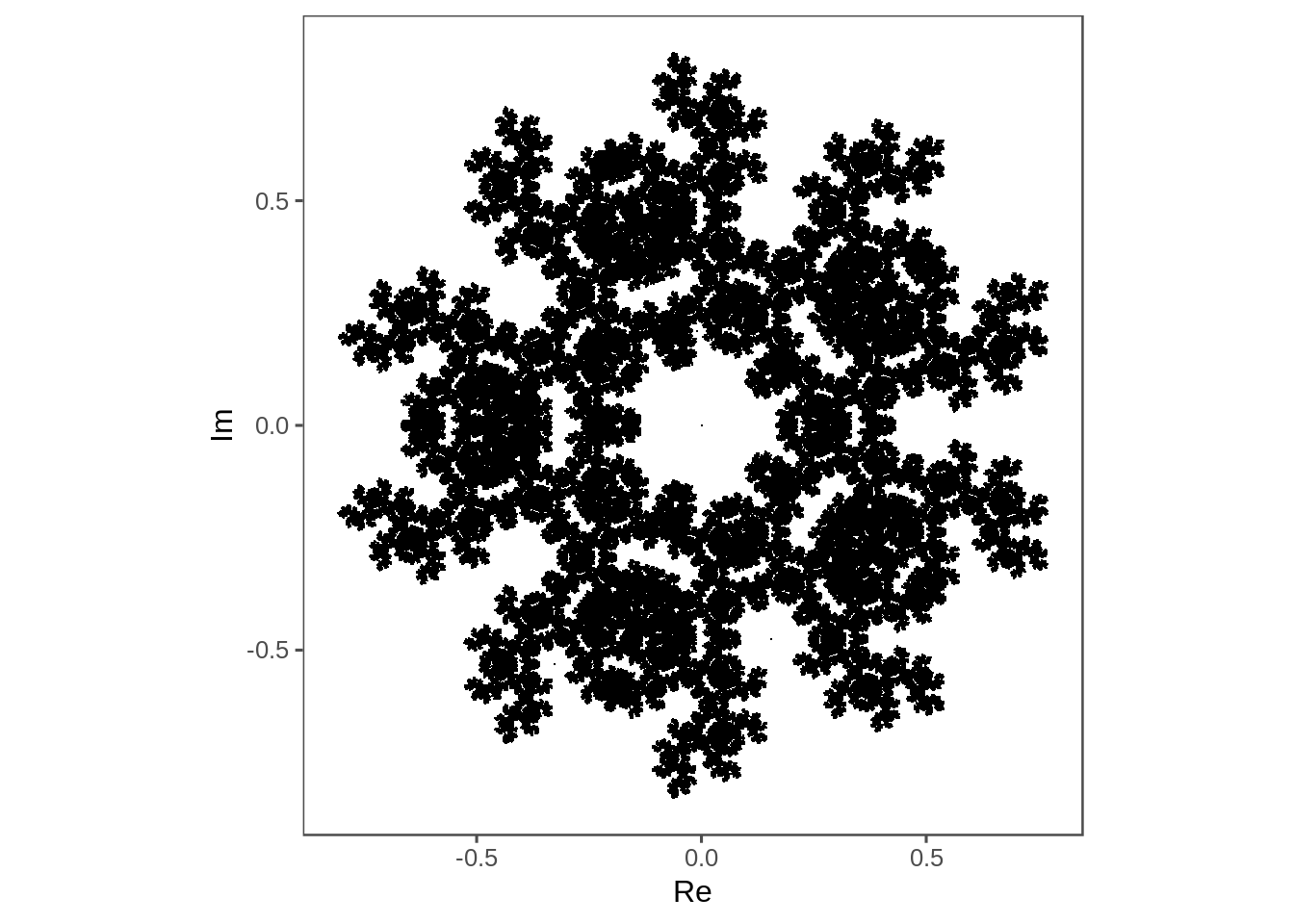

About 1e5 points seems to be the sweet spot.

Let’s call the Chaos Game without restrictions ‘normal’ and make a function for the normal chaos game on the n-gon.

normal_chaos_game <- function(n_gon, number_of_points=1e5){
  
  polygon <- poly(n_gon)
  
  points <- rep(0i, number_of_points) #slightly better than always extending the lists.
  
  chosen_vertex <- sample(seq_len(n_gon), number_of_points, replace = T)
  
  for(i in 2:number_of_points){
  
    this_vertex <- polygon[chosen_vertex[i]]
    
    points[i] <- (points[i-1] + this_vertex)/2
  }
  
  return(points)
}

normal_chaos_game(3) %>%
  plot_complex_points()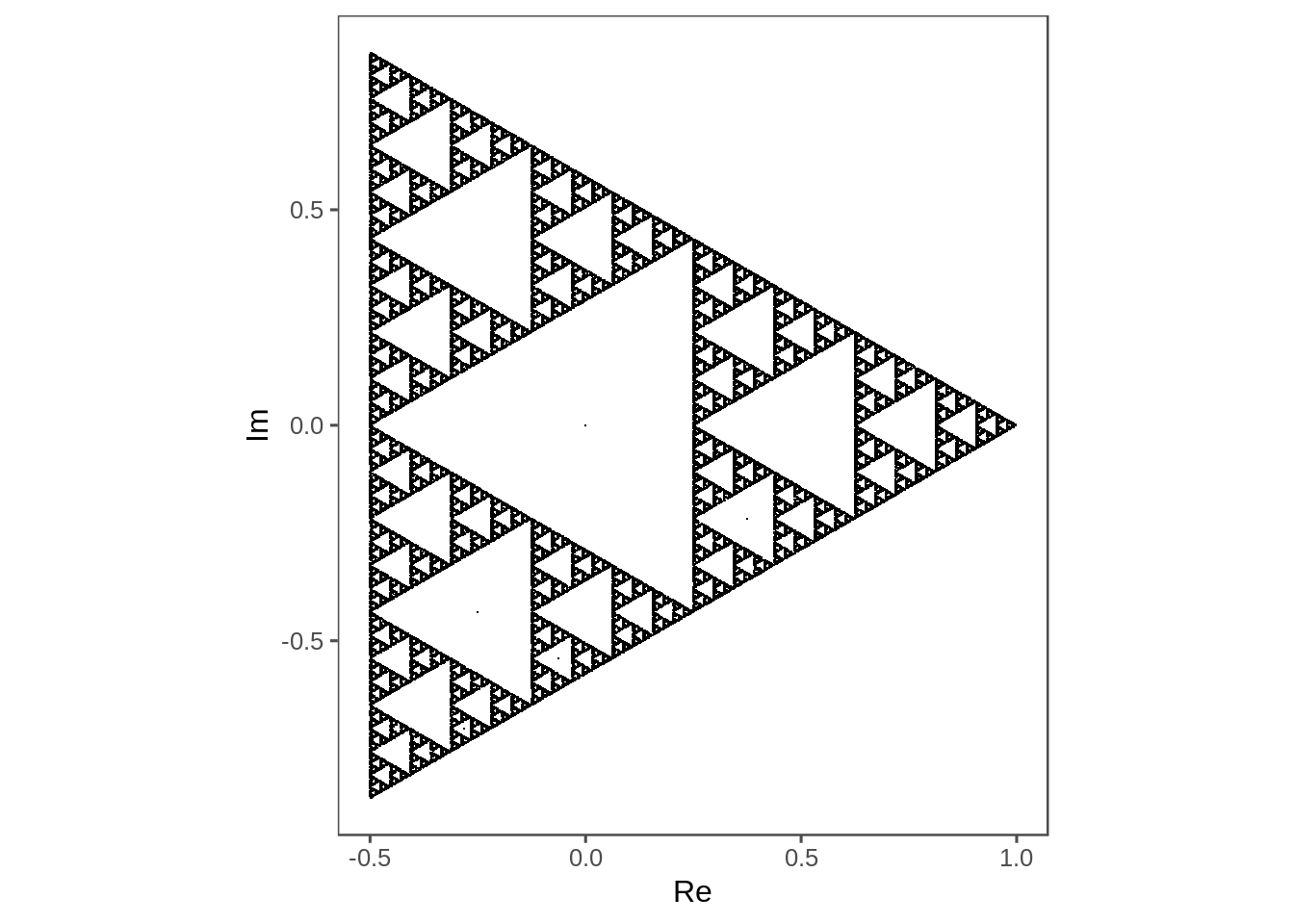

normal_chaos_game(5) %>%
  plot_complex_points()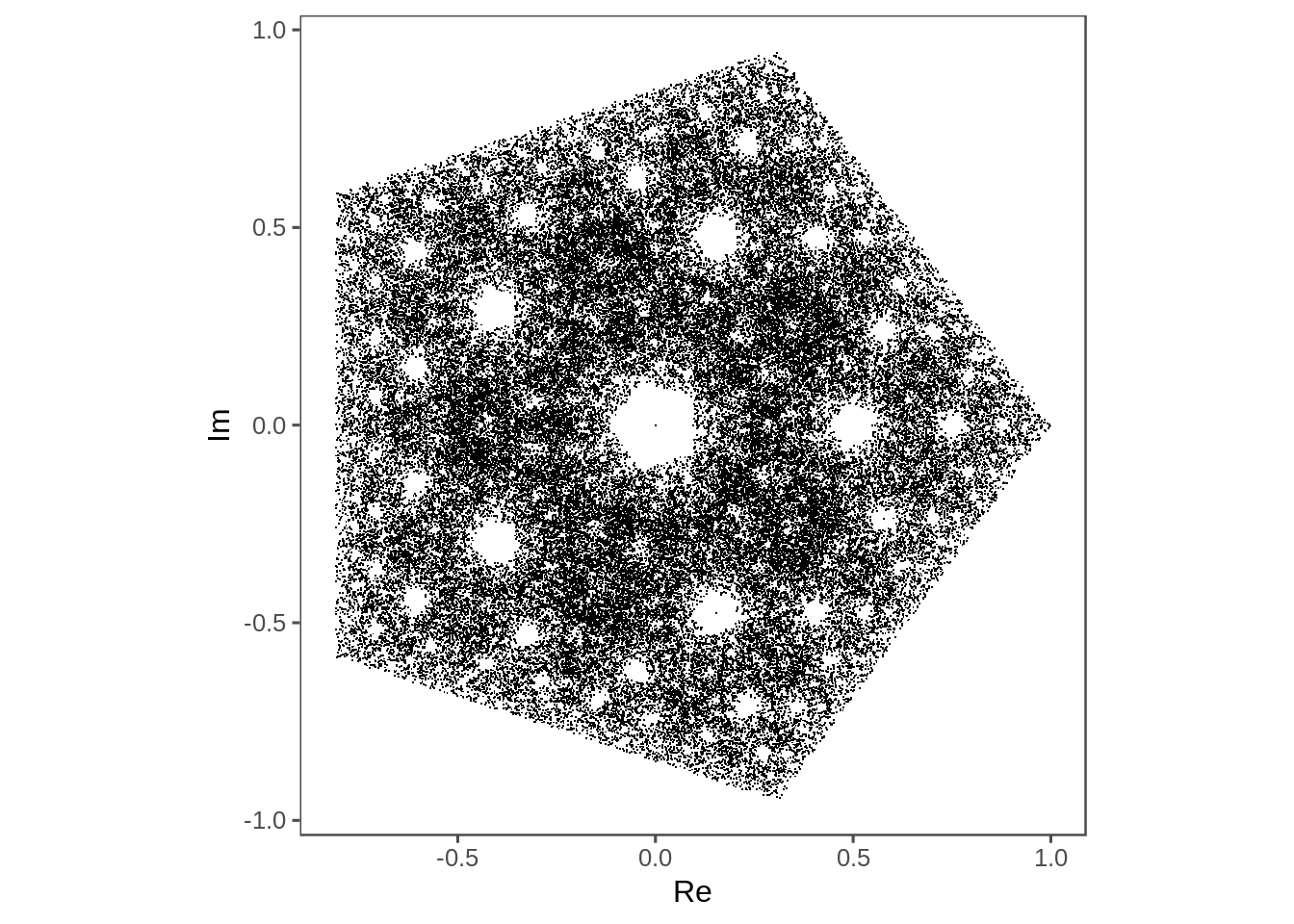

normal_chaos_game(6) %>% #An interesting case, roll a normal die every time!
  plot_complex_points()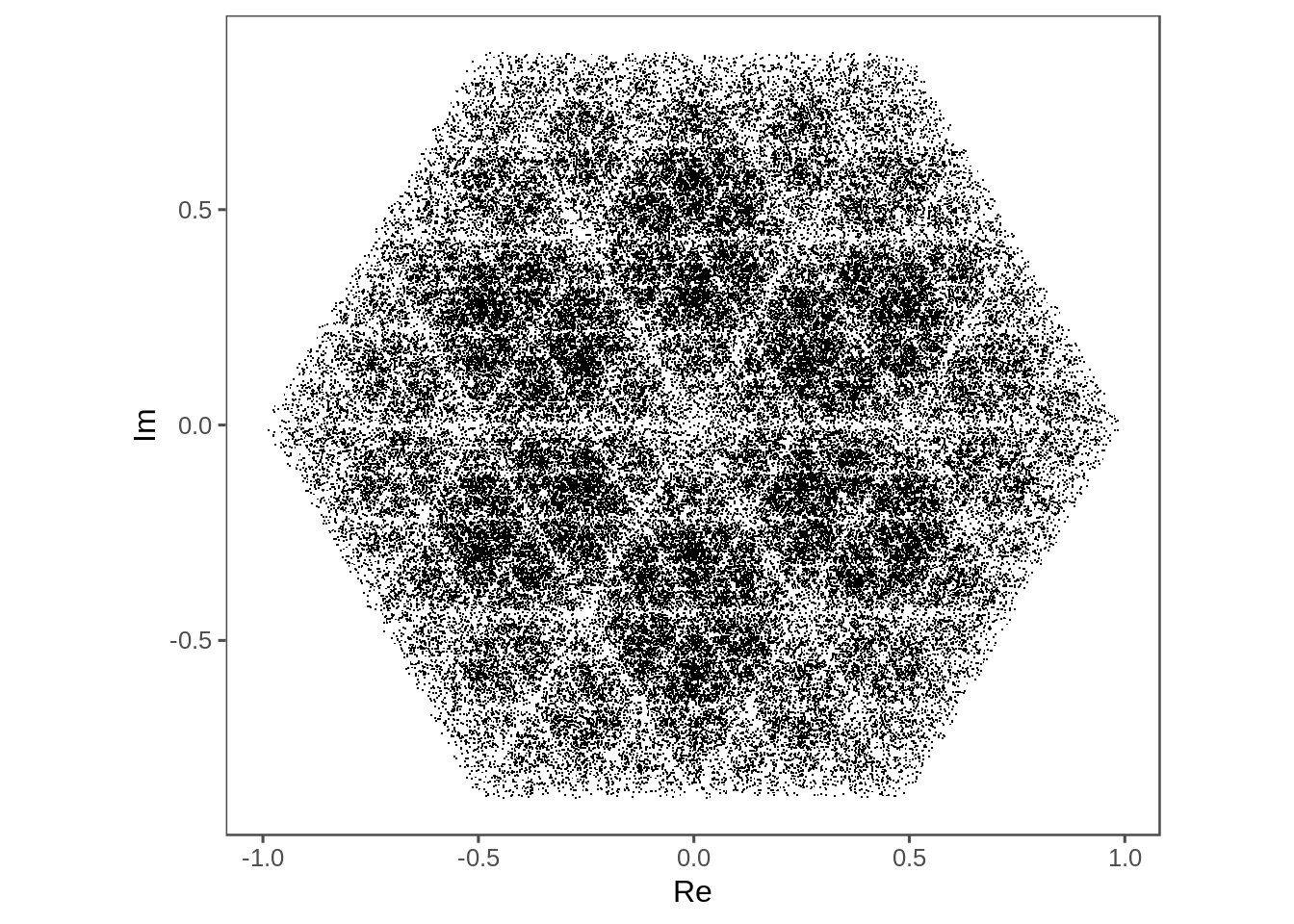

Wiki notes that the square doesn’t work in the normal case, but what about the net of the tetrahedron, or a triangle with another vertex in the middle.

tetrahedron <- c(poly(3), 0i)

points <- rep(0.1i, number_of_points) #slightly better than always extending the lists.
  
chosen_vertex <- sample(1:4, number_of_points, replace = T)
  
for(i in 2:number_of_points){
  
    this_vertex <- tetrahedron[chosen_vertex[i]]
    
    points[i] <- (points[i-1] + this_vertex)/2
}

plot_complex_points(points)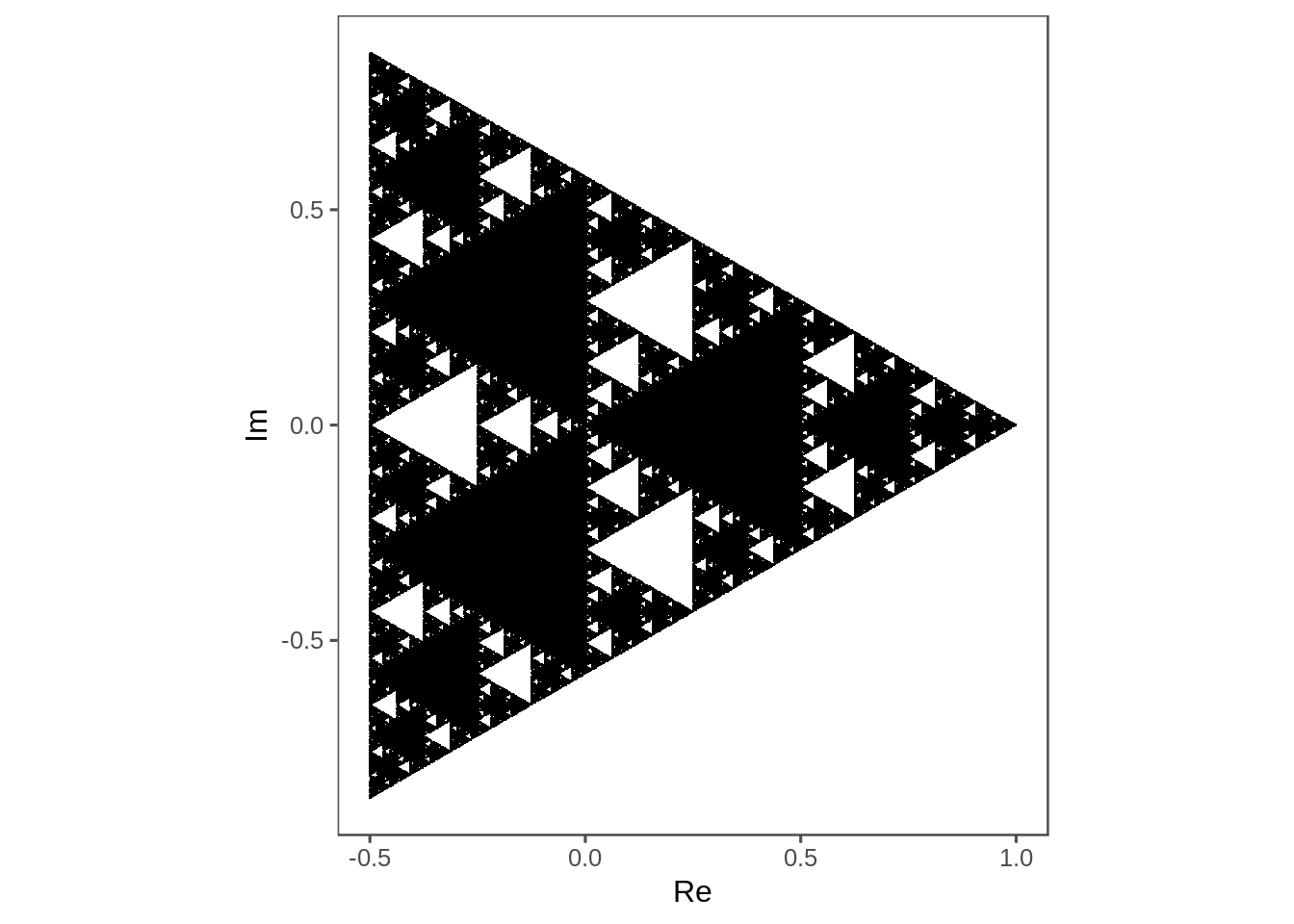

This… confuses me. It’s very Escher.

If the rule is “not the last one”, then we can get some more.

not_last <- function(n_gon, number_of_points=1e5){
  
  polygon <- poly(n_gon)
  
  points <- rep(0i, number_of_points) #slightly better than always extending the lists.
  
  chosen_vertex <- sample(0:(n_gon-2), number_of_points, replace = T)

  chosen_vertex[1] <- chosen_vertex[1] + 1
  for(i in 2:number_of_points){
    chosen_vertex[i] <- ((chosen_vertex[i-1] + chosen_vertex[i]) %% n_gon) + 1

    this_vertex <- polygon[chosen_vertex[i]]
    
    points[i] <- (points[i-1] + this_vertex)/2
  }

  return(points)
}

not_last(3) %>%
  plot_complex_points()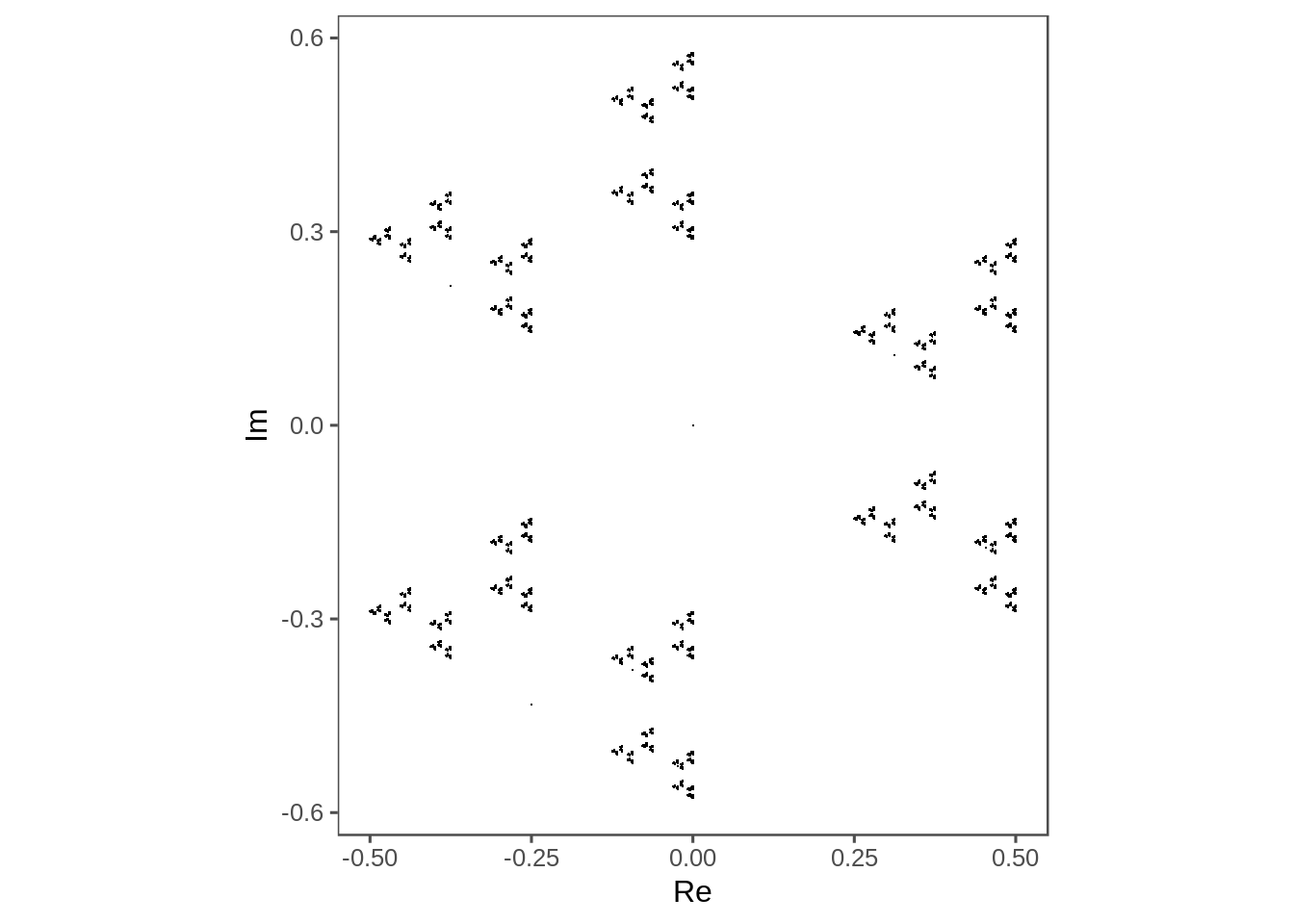

not_last(4) %>% 
  plot_complex_points()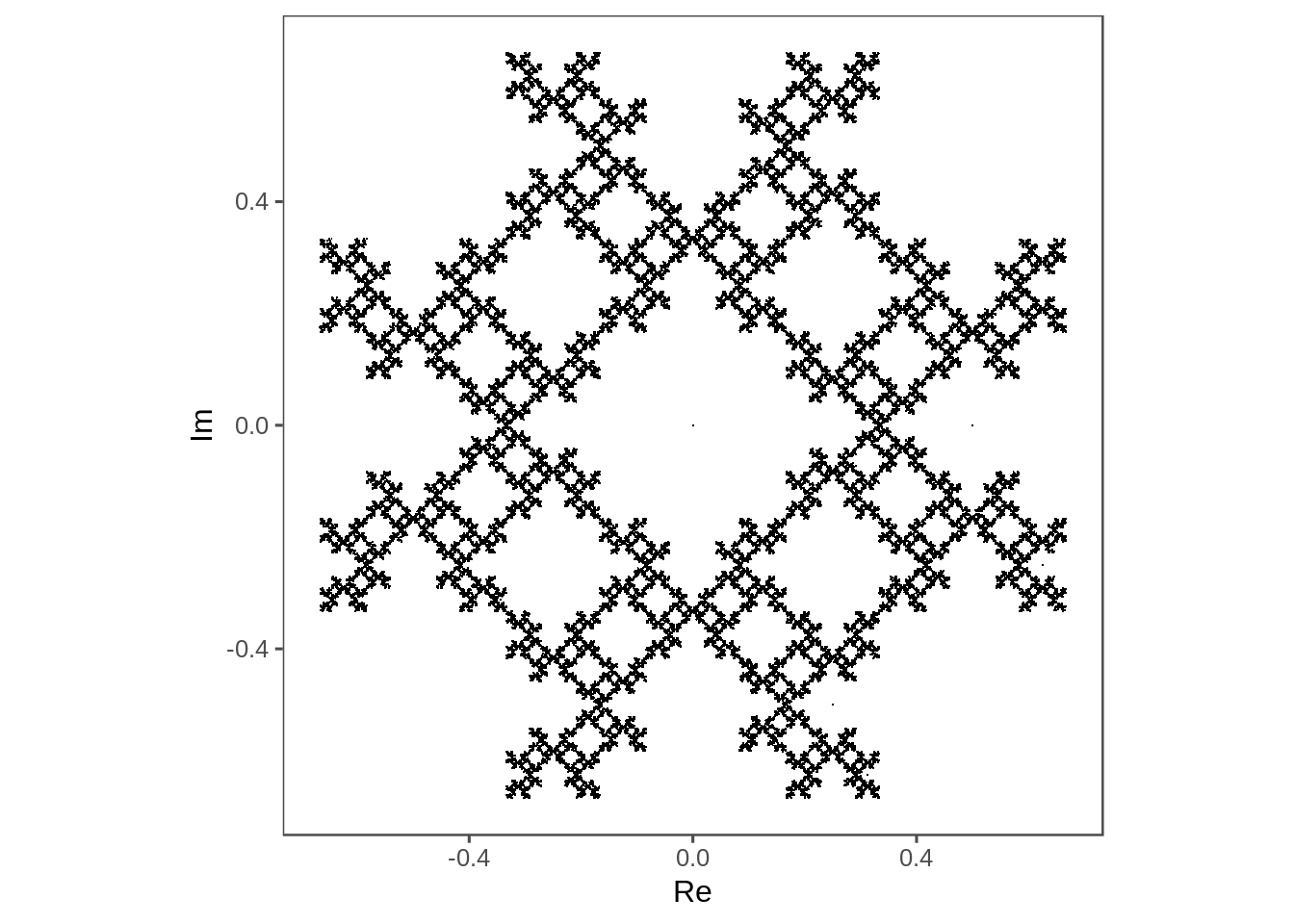

not_last(5) %>% 
  plot_complex_points()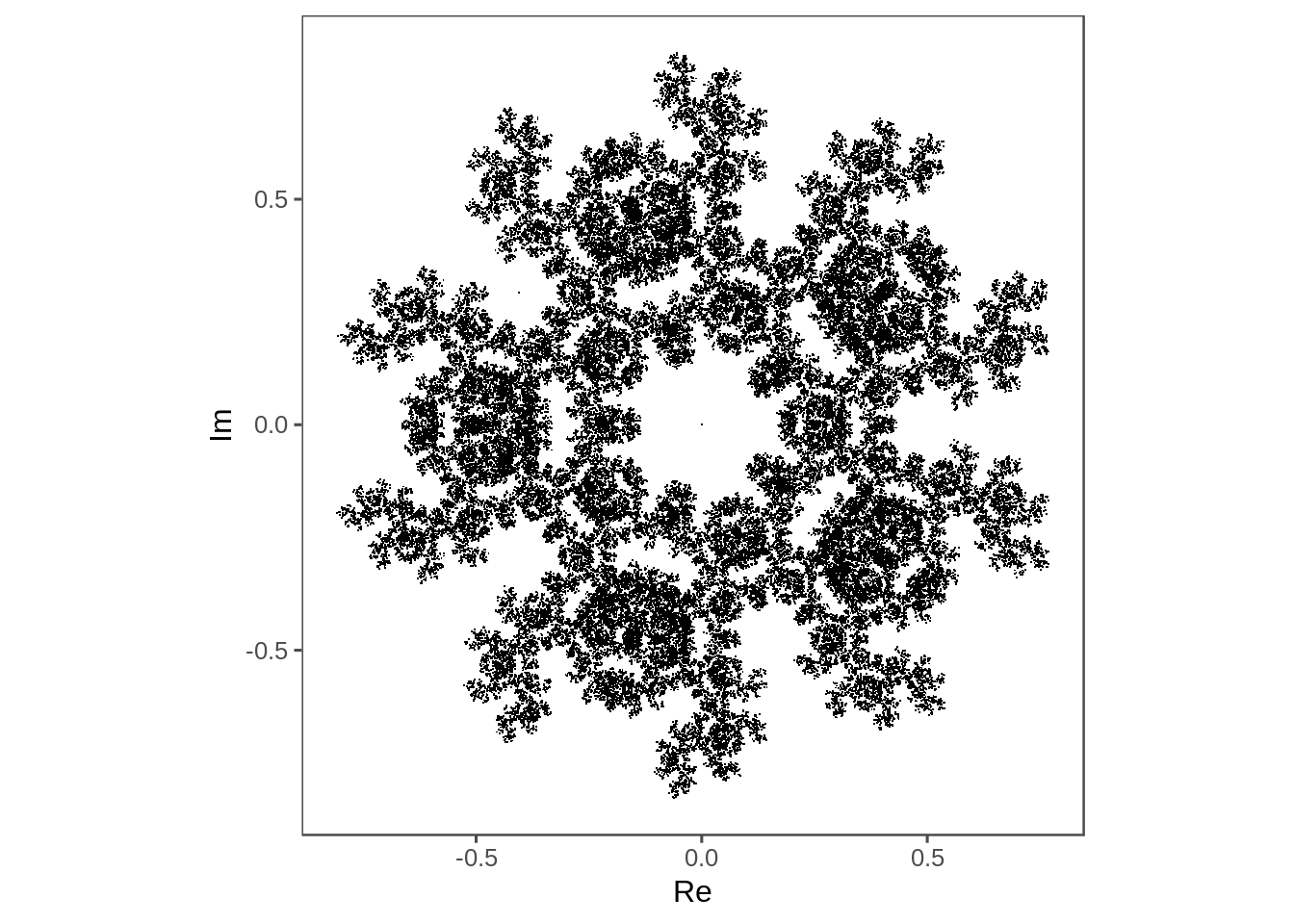

not_last(6) %>% 
  plot_complex_points()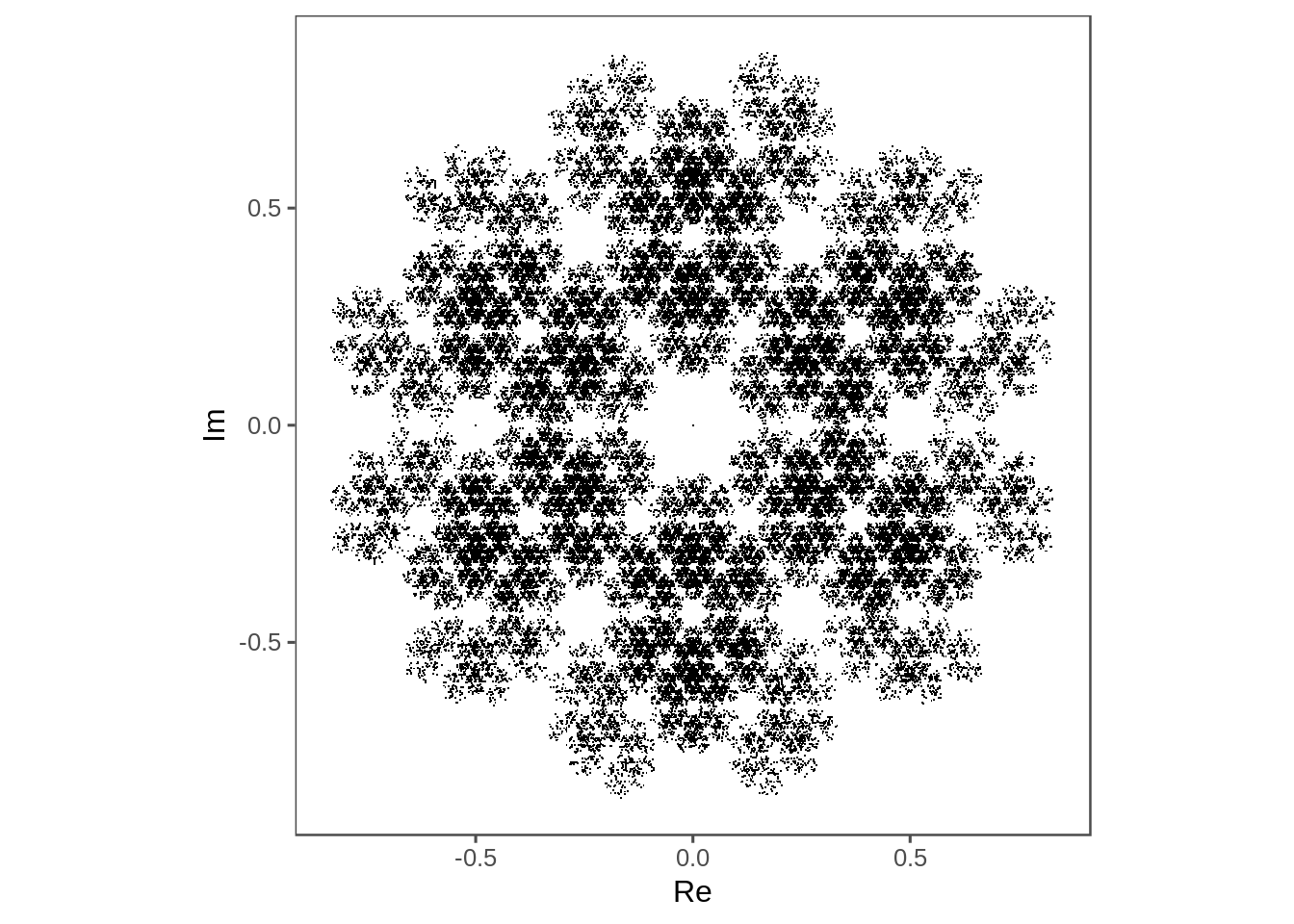

Wiki also shows off some where the rule is “not adjacent to the the last 2 choices (but the same is AOK)”. I’m going to abandon efficency of code running, and make a loop with dice rolls.

not_adjacent_last_two <- function(n_gon, number_of_points=1e5){
  
  polygon <- poly(n_gon)
  
  points <- rep(0i, number_of_points) #slightly better than always extending the lists.
  
  chosen_vertex <- rep(1, number_of_points)
  
  ##Handle the first 2 points specially
  points[2] <- (points[1] + polygon[chosen_vertex[1]])/2
  
  
  for(i in 3:number_of_points){
    bad_choices <- c(chosen_vertex[i-1] + 1,
                     chosen_vertex[i-1] - 1,
                     chosen_vertex[i-2] + 1,
                     chosen_vertex[i-2] - 1) #map might have been more robust, but this is easier to read.
    
    bad_choices <- ((bad_choices - 1) %% n_gon) + 1 ## Really should have considered 0-indexing polygon points
    
    good_choices <- setdiff(seq_len(n_gon), bad_choices)
    chosen_vertex[i] <- sample(good_choices, 1)
    
    this_vertex <- polygon[chosen_vertex[i]]
    
    points[i] <- (points[i-1] + this_vertex)/2

  }
  return(points)
}

not_adjacent_last_two(6) %>%
  plot_complex_points()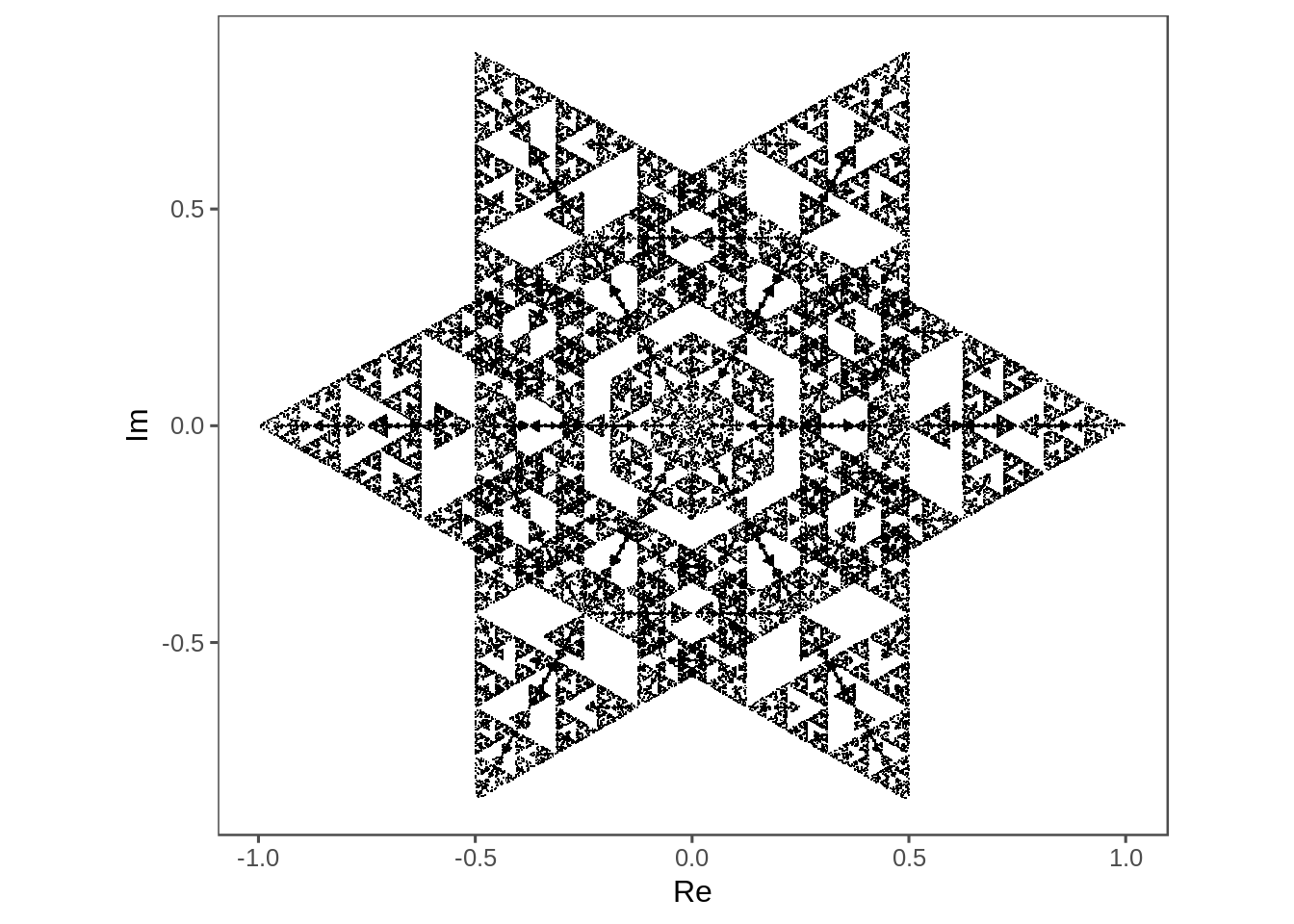

Wow.